SPINNING TOPS, GYROSCOPES &
RATTLEBACKS
Rod Cross, Dec 2017

A spinning top is not just a child’s toy. It is also an adult toy, in the sense that it helps to have a PhD in physics to figure out how it works. Besides, some adults DO play with spinning tops (check the web), and some make very elegant ones (see www.puccimanuli.com under spinners). A spinning top is remarkable because it tends to defy gravity while it is spinning. If spun fast enough, a spinning top will rise to a vertical position and happily stay there, despite the fact that it will fall over if it stops spinning.
A spinning egg is just as amazing. If a hard-boiled egg is spun fast enough it will rise up and spin on one end. A tippe top does something similar, but is even more spectacular. It turns itself completely upside down and ends up spinning with its peg underneath the sphere that was originally spinning underneath the peg used to spin it.
The basic physics behind all these effects is that a torque is required to rotate an object. The torque is equal to the rate of change of angular momentum. There is nothing magic about that. It is the rotational equivalent of what happens when an object accelerates along a straight line. In that case, the force on the object is equal to the rate of change of its momentum. Angular momentum is similar to linear momentum, but it refers to motion in a circular rather than a straight line path.
Usually, the torque acting on a spinning top is just due to the weight of the top. If the top is perfectly upright there is no torque acting on it but if it leans sideways then it will tend to fall over due to the torque about the bottom end. It will indeed fall over if it is not spinning. If it is spinning then it does something else. Instead of falling down, it “falls” sideways. That’s the amazing part. The effect is described as precession, and is explained in simple terms below. A spinning top precesses slowly around a vertical axis through its point of support while it spins rapidly about its own axis. The usual “explanation” is that the change in angular momentum must be in the same direction as the torque on the top – that is, in the sideways direction. The spin axis must move sideways instead of down, but that is just stating the observed facts in fancy technical words.
The following slow motion video clips show what happens with different types of tops, including a spinning egg and two types of tippe top. The tops were filmed at 300 fps to measure their spin and rate of precession. You will see the tops spinning ten times slower than they actually did. The first two are a 100 gram aluminium disk with a pointy bottom end, viewed from the side and the top (just before it fell). The third and fourth is the same disk supported on a round, brass knob. The bottom end makes a big difference. The brass end top takes a while to stand up straight, as shown in the fourth video clip. Its centre of mass rises slowly since the brass ball rolls and the friction force at the bottom end is relatively small. It is the torque generated by friction at the bottom end that causes tops to rise upward and defy gravity. However, all tops eventually fall when the spin drops to a low value. Further details can be found in “The rise and fall of spinning tops”, Am J Phys 81(4), 280-289 (2013).
Here is a spinning hollow plastic egg, a solid wood egg and a solid aluminum egg. The plastic egg was spun at a low speed and didn’t stand upright, but that was done deliberately to record its motion at low speed. It precesses at two different frequencies at the same time, about two different vertical axes. It precesses quickly about a vertical axis through the middle of the egg and precesses slowly about a vertical axis located outside the egg. The wood egg was spun faster and stood up higher. All three eggs rise as a result of sliding friction until they start rolling and then the precession frequency is about the same as the spin frequency – unlike a sharply pointed top where the precession frequency is much smaller than the spin frequency.
In order to understand the behaviour of a spinning egg, it is necessary to understand the effect of the forces on the egg. Here are three more slow motion video clips showing what happens when an egg falls from rest and when an egg is spun very slowly. The only forces on the egg are gravity, the normal reaction force and friction, but all three videos contain some surprises.
If an egg is on its fat end when it falls, it slides forward. On its pointy end, the egg rolls right over then slides. The egg has more potential energy when the fat end is at the top, so there is more kinetic energy when it falls. If the fat end remains at the bottom after falling, then the thin end can rotate all the way up to the top with enough energy left over to swing it past the top.
Spun slowly clockwise, the egg precesses in a counter-clockwise direction, rocking from one end to the other, in the same way that people move heavy furniture. If you look carefully, you will see that the egg spins slowly about its long axis. Check out the position of the dot on the pointy end each time the pointy end points to the camera. That is the best way to measure the spin about the long axis. It is smaller than the spin about the vertical axis. The egg is sliding rather than rolling on the horizontal surface in this case so there is a relatively large friction force on the egg.
See also “Spinning eggs and ballerinas”, Physics Education, 48(1), 51-56 (2013).
A tippe top not only inverts itself, it can become airborne as it does so. The effect is shown in the following slow motion video clip. Also shown are two spherical tippe tops. The usual tippe top has a peg on top to spin it, and its centre of mass is located below the centre of curvature. For that reason, a tippe top stands upright when placed at rest on a horizontal surface. If a small mass is located inside a hollow sphere, then the centre of mass is shifted away from the middle of the sphere. It also works nicely as a tippe top. The green sphere has a small piece of blu-tak in the bottom. The red/white sphere has two metal nuts near the middle, screwed onto nylon thread. In all three cases, the centre of mass rises when the tops are spun.
For further details, see “Spherical Tippe Tops” in The Physics Teacher, 51(3), 144-145 (2013).
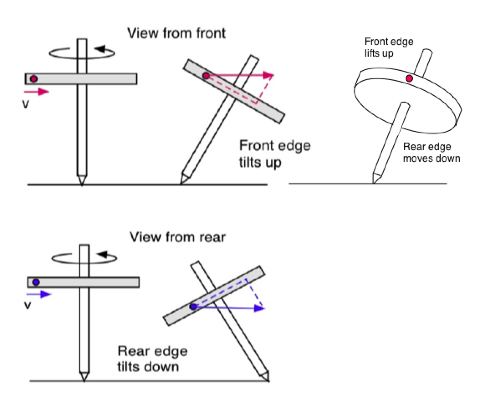
A simple explanation of precession can be given in terms of the diagrams below. Suppose that a top is spinning counter-clockwise viewed from above and suppose it is upright, as drawn on the left side of the diagram. Now suppose that gravity causes the top to fall to the right, as viewed from the front. Viewed from the rear, the top falls to the left. The red dot on the front edge represents a small part of the top, and it is moving left to right at high speed. The blue dot on the rear edge of the top is also moving left to right at high speed, when viewed from the rear. Any object that is moving at high speed left to right will continue moving left to right due its momentum, although it can also move up or down if an up or down force is exerted while it is moving. For example, a bullet fired horizontally will continue to move at high speed in a horizontal direction while it falls slowly to the ground under the influence of the vertical gravitational force.
Gravity causes the whole top to tip to the right when viewed from the front, but the red dot will tend to move in a straight line since it is moving at high speed. Imagine that the red dot is a small bullet attached to the disk. The result is that the front edge of the disk lifts upward as the disk falls. The two dashed lines represent the components of the velocity vector – one parallel to the edge of the disk and one perpendicular, showing the front edge lifting up.
Similarly, the momentum of the blue dot tends to carry it forward in a straight line. As a result, the rear edge of the top tilts down. The whole top therefore tilts up at the front edge and down at the rear edge, which means that the top tilts into the page when viewed from the front. That is why the top precesses by moving sideways (into the page) when it is spinning rather than falling straight down due to gravity. At least, that is how precession gets started when a spinning top starts falling. With steady precession, there is no falling motion at all.
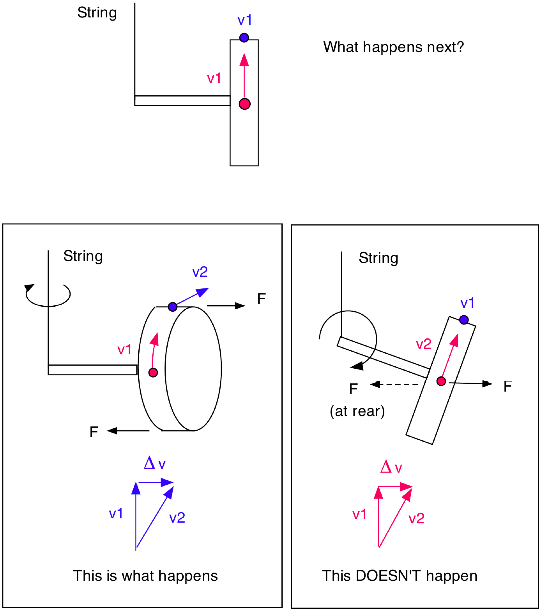
Here is a simple gyroscope filmed at 600 frames/sec. The disk rotates once every 10 frames or in 10/600 seconds, so it spins at 60 Hz or 3600 rpm. It precesses once in 1400 frames or in 1400/600 = 2.3 seconds so it precesses at 0.43 Hz or 26 rpm. The mass of the brass disk is 108 grams, and its diameter is 56 mm. The left end is supported by a length of string. The axis is slightly above the horizontal since the disk is spinning so fast. It drops below the horizontal as it slows down. The other end bobs up and down rapidly due to nutation. The string swings out from the vertical to provide a centripetal force on the gyro since the gyro rotates slowly in a circular path about the vertical axis.
You can watch it for as long as you like, and it won’t fall down. That is simply amazing. It looks like a magic trick with a hidden spider thread holding up the other end. The torque about the center of mass is directed into the screen in the photo. The angular momentum of the disk lies along the spin axis and points to the end supported by the string. The change in the angular momentum points into the screen, since that is the direction of the torque, meaning that the tip of the angular momentum vector moves into the screen and the opposite end moves out of the screen towards you. It still looks like magic, especially since the film is viewed in slow motion and the disk seems to be rotating at low speed.
Here is another explanation. The red particle is moving up at velocity v1 and the blue particle at the top is moving into the screen at velocity v1. What happens next? The disk could rotate out of the screen or it could rotate downwards, which is the intuitive expectation. In the first case, the velocity of the blue particle changes direction (but not magnitude) to v2 but the velocity of the red particle doesn’t change since it continues to move upward at speed v1 even if the disk rotates out of the screen. And vice-versa if the disk rotates downwards. The change in v is directed left to right in each case, as shown in the diagrams below, so there must be a left to right force F on the particle to change its velocity. The two F’s shown in each diagram (top and bottom or front and rear) are in opposite directions, meaning that there is a torque on the disk. The torque is due to the string pulling up on the axle and it acts in a direction into the screen. That is how the two F’s are acting when the disk rotates out of the screen. If the disk rotated down the screen the two F’s would generate a torque about the vertical axis. There is no such torque acting on the disk, so this can’t happen – unless a horizontal force is applied to the axle in an attempt to reduce the precession frequency. A horizontal force applied to increase the precession frequency would cause the disk to rise.
Here is a gyroscope from www.gyroscope.com Click the image to see it precess. If the wheel is not spinning then the counter-balance at the opposite end is not heavy enough to hold the wheel up. If the wheel spins, the gyro generates an upward torque to balance the counter-weight, and the gyro precesses slowly. The upward torque is proportional to the precession frequency. If the support is pushed horizontally to speed up the precession, the gyro rises vertically since the upward torque increases.
In 1974, Professor Eric Laithwaite showed that he could lift an 18 kg disk above his head, using one hand, when the disk was spinning on the end of a 0.9 m long axle. In Feb 2014, Derek Muller repeated the experiment. The disk acts a gyroscope and precesses in a horizontal plane rather than falling vertically. If the disk was not spinning, it would be impossible to support the disk in that manner. I filmed the “Herculian” effort at 300 fps. Note that Derek pushes the axle horizontally at the start to speed up the precession so that the disk rises more easily.
YouTube videos of the experiment can be found at http://youtu.be/GeyDf4ooPdo and http://youtu.be/tLMpdBjA2SU
If you spin an object on a table, then friction will slow it down until it comes to a stop. A rattleback not only slows down to a stop but it then reverses direction. There are many theoretical papers on the subject and many videos of rattlebacks on YouTube, but there are no simple explanations. All existing explanations are very mathematical and quite obscure. Nevertheless, there is a simple explanation, and it involves the effect of friction. You can make your own rattleback by cutting the handle off a plastic spoon and attaching two small masses to each end of the spoon. The secret of a rattleback is that the distribution of mass is not lined up with the geometric axis. So, the two small masses must be located as shown in this 3Mb QuickTime slow motion video taken at 300 fps. I used two small pieces a Blu-Tack, a re-usable adhesive.
If you look carefully you will see that the spoon rocks from side to side and from end to end while it rotates. The sideways rocking motion and the end-to-end motion is correlated rather than being independent. I attached a thin wire to the spoon, along its axis, to see the motion more clearly. When the spoon tilts sideways, it tends to slip sideways on the the table. The same thing would happen if you tried to balance a pencil on one end on the table and tilted it sideways slightly so that it falls. The bottom end of the pencil would either slide on the table or pivot about the bottom end, depending on the coefficient of friction. Friction acts in the opposite direction to motion of the bottom end. If the pencil pivots about the bottom end, static friction prevents the bottom end from sliding.
Now, look carefully at the video. At one point near the beginning, the spoon actually slides on the table, but mostly it doesn’t because static friction prevents it sliding. That friction force acts to rotate the spoon in the direction you see it rotating, even if there is no rotation at the start. The spoon therefore has a preferred direction of rotation. If you start it rotating the other way, the spoon will stop rotating and start rocking (to conserve energy) and it then starts rotating the other way. In the video I started the spoon rocking by pushing down on one end and then releasing the spoon. There was no rotation at the start.
There is an even simpler explanation. Any object weighted on one side will tend to fall to that side when it is allowed to fall. Here is a curved aluminum strip with an offset bolt at each end. When the strip rocks from one end to the other, it falls to the heavy side so the whole strip rotates in that direction. If the strip was also curved in the sideways direction, like a spoon, it would rotate more freely. However, a long strip like this would topple over sideways since it would be too top heavy.
See The Physics
Teacher, 51(12),
544-545 (2013) for further details.
SUMMARY
Brass disk on P800 emery paper at 300 fps
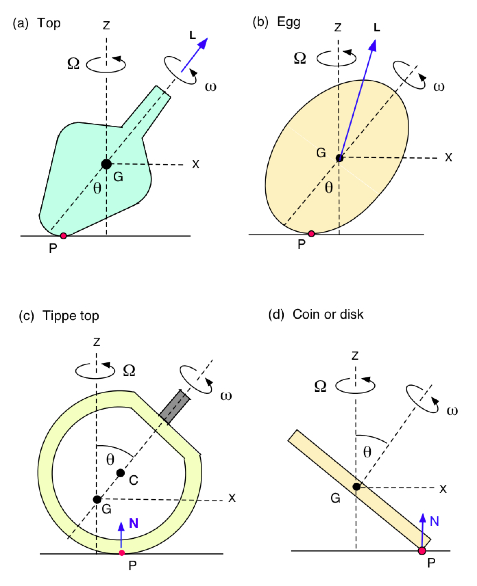

All four objects here are
spinning on a horizontal surface, all precess at angular velocity \Omega about
a vertical axis (Z) through the centre of mass (G), and all spin at angular
velocity \omega about an axis of symmetry. All are described by Euler’s angular
momentum equation which relates the change in angular momentum to the torque on
the object. The torque has a component due to the normal reaction force N in
the vertical direction (N = Mg) and it has components due to the horizontal
friction force F acting at the contact point P.
(a) The
top rotates with \omega much larger than \Omega and tends to roll on the
surface. The angular momentum vector L points along the spin axis and rises
slowly as the top rises.
(b) The
egg rotates initially with \Omega much larger than \omega so point P slides out
of the page and the sliding friction force on the egg acts into the page. The egg
precesses about the Z axis due to the vertical force in the Z direction, and it
precesses about the Y axis due to the horizontal force in the Y direction. The
egg therefore rises. However, if it is not spun fast enough, sliding eventually
gives way to rolling, F drops to
zero so the egg stops rising. See Eur J Phys Dec 2017.
(c) The
tippe top rotates in the opposite direction to the egg (that is, \theta
increases) since the sliding friction force is in the opposite direction. G
rises since the top precesses about the Y axis due to the friction force in the
Y direction. See Eur J Phys Jan 2018.
(d) A
coin or any other disk rolls on its edge and slowly falls due to slow
precession around the Y axis. As with a rolling ball on a horizontal surface,
there is a small offset in the line of action of N, resulting in a torque that
opposes the torque due to the horizontal rolling friction force.
















