PHYSICS OF TENNIS
The behaviour of racquets and balls is
governed mainly by Newton’s three Laws of Tennis. These laws are fully
explained in our book The Physics and Technology of Tennis. The following is a summary
of a few topics of interest to give you a flavour of how physics relates to
sport and to the real world of everyday objects.
1. The sweet spots of a racquet
A tennis racquet, like a baseball or cricket bat, has
a sweet spot. If a ball impacts at the sweet spot, the force transmitted to the
hand is sufficiently small that the player is almost unaware that the impact
has occured. If the ball impacts at a point well away from the sweet spot, the
player will feel some jarring and vibration of the handle. The sweet spot is a
vibration node, located near the centre of the strings. Another potential sweet
spot is the centre of percussion (COP). These and some other significant spots
on a racquet are shown below.
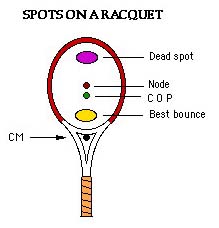
Contrary to
popular opinion, the sweet spot does not coincide with the point at which the
ball rebounds with maximum speed, nor does it locate the spot where the force
on the hand is zero. Forces on the hand arise from three independent motions of
the handle, namely rotation, translation and vibration. The vibrational
component is absent when a ball strikes the vibration node. The rotational
component, arising from recoil of the racquet head, exerts a torque on the
hand, causing it rotate about an axis through the wrist. As a result, a force
is always exerted on the upper part of the hand, and a force in the opposite
direction is always exerted on the lower part of the hand.
The COP shown
in the diagram above is located close to the node point when the racquet is
freely suspended, but it shifts into the throat area of the racquet when the
racquet is held in the hand. Consequently, the COP shown in the diagram is NOT
the sweet spot that players talk about.
The first two vibration modes of a freely suspended
tennis racquet are shown below. A racquet behaves like a uniform beam in this
respect, despite its round head, since the centre of mass of a racquet is near
the centre of the racquet. The fundamental mode has a frequency of about 100 Hz
for a relatively flexible frame or about 180 Hz for a stiff frame. One node is
near the centre of the strings, and the other node is in the handle. It is easy
to hear this vibration if you hold the handle lightly at the node in the
handle, with the handle near your ear, then strike the frame or strings. The
vibration node on the strings is easily located using this technique. If you
hold the handle firmly, the frame vibrations (but not the string vibrations)
are strongly
damped.
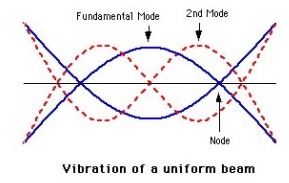
The next mode, for a uniform beam, has a frequency
2.75 times the fundamental frequency. It is not excited with any significant
amplitude since the impact duration, T, of the ball on the strings is about 5
ms. The frequency spectrum of this pulse, approximately a half sine waveform,
peaks at zero frequency and is zero at f = 1.5/T = 300 Hz , close to the second
mode frequency. The impact will still excite string vibrations at about 500 Hz
since the strings are not as strongly damped as the frame.
|
|
|
|
A metal tube will vibrate nicely when struck with a metal rod, but it does not vibrate when struck with a tennis ball. How come? The impact duration, about 0.005 sec, is too long to excite any vibration with a period shorter than about 0.002 sec, especially if the tube is struck at the fundamental vibration node (its sweet spot). |
|
SEE a
racquet vibrate
The vibration of a racquet is
usually too small to see by eye, but a cardboard racquet vibrates the same way and
shows the vibration modes clearly (see photo below). The top end was vibrated
back and forth by about 1 mm at a frequency of about 30 Hz. The nodes in the
frame and in the two strings are easily seen. The photo on the left is with the
vibration generator switched off.
HEAR a
racquet vibrate
The vibration frequency of a
racquet depends on the stiffness of the frame. This is one way of determining
whether you are using a stiff or a flexible racquet. A stiff racquet vibrates at
180 Hz or more. A flexible racquet vibrates at 140 Hz or less. QuickTime sound
files for a racquet held near the ear and tapped by finger or by a ball near
the tip are attached for frequencies of 120,
140, 160,
180, 200 and 220 Hz. These sounds are too low in
frequency to be heard properly using the internal speakers of a computer. You
will hear only some metallic clicks when the racquet is struck. Internal
speakers usually have almost no bass response. You will need to connect
external speakers, with fresh batteries if they are battery operated.
FEEL a
racquet vibrate
The best way to feel a racquet
vibrate is to hit a ball on the tennis court. What is it that you “feel”? Does it feel good or bad? Why do different racquets feel
different? Does a $400 racquet
feel a lot better than a $100 racquet, and if so in what way does it feel better?
These are not easy questions to answer. I have never heard a good explanation
or description in terms of the physics of feel. Players say that some racquets
feel more powerful than others, but how do they know unless they measure the
ball speed, which they don’t?
Can you feel the difference between
a 140 Hz vibration and a 160 Hz vibration? One way to test this is to put your
hand on the speaker used to play the sound files. It will help to use an
external speaker rather than the inbuilt speaker in your computer. You can feel
a thump every time the racquet is hit but that’s because you can easily feel
the change in amplitude (or size) of the vibration. I find that high
frequencies tickle my hand more than low frequencies, especially if the soft
part of the palm of my hand rests gently on the speaker.
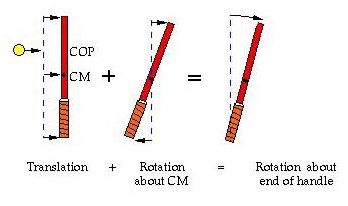
3. Centre of Percussion
Consider a racquet that is freely suspended by a long
length of string or balanced vertically on the end of its handle. If a ball
impacts at the centre of mass (CM), the racquet will recoil at a speed V. All
parts of the racquet will recoil at the same speed V. If the ball impacts at
any other point on the strings, the racquet will recoil and it will also rotate
about its CM. The whole racquet then moves away from the ball with a speed V1
due to the recoil , but the handle simultaneously moves towards the ball with
speed V2 due to rotation of the racquet. If there is any point in the handle
where V1 = V2, then that point will remain stationary and the rest of the
racquet will rotate about that point as shown below.
The axis of rotation is called the conjugate point
with respect to the impact point, and the impact point is called the centre of
percussion (COP) for that particular axis of rotation. The axis and the COP
form a pair of conjugate points. For an impact near the tip of the racquet, the
axis of rotation is about half way between the end of the handle and the CM.
For an impact near the throat of the racquet, the axis of rotation is beyond
the end of the handle.
Now consider a racquet that is suspended by a rod
passing through a hole drilled through the handle so that the racquet can
rotate freely about this axis when a ball strikes the strings. When a ball
impacts on the strings, the handle will exert a force on the axis unless the
ball impacts at the COP. Consequently, the COP is often regarded as a second
sweet spot since the force on the hand should be zero for an impact at the COP.
However, the hand adds an additional mass of about 500 gram to the handle, and
it shifts the location of the COP to a position near the throat area of the
racquet. The details of this
effect are described in an Am J. Phys article that you can download here.
4. The dead spot of a racquet
Clamp the end
of the handle on a table, using your hand to press on the handle, so the rest
of the racquet hangs over the edge of the table. Then drop a ball onto the
strings at various points. The ball will bounce best near the throat. There is
a spot near the tip where the ball doesn't bounce at all. That's the dead spot.
At the dead spot, all of the energy of the ball is given to the racquet, and
the racquet does not give any energy back to the ball. The reason is that the
effective mass of the racquet at that point is equal to the mass of the ball.
The effective mass is the ratio of the force at that point to the acceleration
at that point (F = ma so m = F/a). If a ball of mass m collides head-on with
another ball of mass m at rest, then the incident ball stops dead and gives all
its energy to the other ball.
Similarly,
if a moving racquet strikes a stationary ball at the dead spot, then all the
rotational energy of the racquet is given to the ball. A good place to hit a
ball when serving is near the dead spot. However, when returning a fast serve,
the dead spot is the worst place to hit the ball. The best spot is nearer the
throat of the racquet since that's where the ball bounces best.
5. Tennis
balls
The rules of
tennis specify that the ball must bounce to a height between 53 and 58 inches
when dropped from a height of 100 inches onto a concrete slab. What happens in
actual play is hard to predict, but a good test is to drop a ball onto the
strings when the head is clamped (eg by placing the racquet on the floor and
stepping on the handle near the head). When dropped from a height of say 1
metre, the ball will bounce to a height of about 0.70 metre. The ball loses
about 45% of its energy when dropped on concrete, but it loses only 30% of its
energy when dropped on the strings. That's because the strings absorb some of
the impact energy and then give almost all of that back to the ball. The amount
of energy lost by the ball depends on its compression. When dropped from 100
inches on concrete, it compresses by about 6 mm. When dropped on the strings,
it compresses by about 3 mm. The bigger the compression, the more energy is
lost when the ball expands back to its original shape. That means that at high
impact speeds, where the ball compresses more, the energy loss is even greater.
Furthermore, the fraction of the ball's energy that is lost also increases as
the the ball's energy is increased or as the compression is increased.
6. Ball Spin
The modern
game of tennis is dominated by the amount of spin that players can impart to
the ball. The change from small 9 inch heads in wood racquets to large 10.5
inch heads in graphite racquets allowed players to hit with more topspin since
the ball was less likely to clip the frame. This also allowed players to hit
the ball harder since balls hit with topspin dive down more sharply onto the
court after they clear the net. By hitting the ball harder, players generated
even more topspin, which allowed them to hit the ball even harder. The modern
game is played at a much faster pace than in the wood racquet era, not because
modern racquets or players are more powerful but because racquet heads are now
an inch or two wider, allowing players to hit the ball with much more topspin.
To extract as
much topspin as possible from a stroke, players have learnt to swing up at the
ball and to tilt the racquet head forward, That way, a ball coming off the
court with topspin can be returned with topspin. The spin direction must be
reversed to achieve this result. Two QuickTime movie files are attached showing
how this is done, one by myself and one by Federer. The physics of each shot is the same, the
only real difference being that Federer has a more elegant style. The film of
Federer was taken at about 1000 frames/sec judging by the fact that the ball
sits on the strings for about 5ms and is seen for 4 or 5 frames on the strings.
The amount
of spin depends on a whole bunch of factors, including the speed, spin and
angle of the incident ball, the speed, approach angle and tilt of the racquet,
the type of string etc. If the ball is rising at the same speed as the racquet,
then no topspin will be generated, as shown in this movie
clip, since the racquet does not brush upwards against the back of the
ball. It is clear from this result that more topspin will be generated if the
player strikes the ball while the ball is falling, rather than when the
incoming ball is rising.
Detailed
measurements and calculations of ball spin off different strings, as well as
movie clips showing the results, can be found at http://twu.tennis-warehouse.com/learning_center/spinexperiment.php
(NEW
APRIL 2010)
7. PowerPoint Presentations and Movies
I often get requests from students
wanting ideas for experiments or projects relating to the physics of tennis. I
have prepared a few PowerPoint presentations
on this subject, including some of the basic physics behind each experiment.
They can be viewed directly on the web or downloaded as .ppt files. This page
also contains some movies concerning various tennis experiments.
7. Further
reading
Brody, H. (1979) Physics of the tennis racket.
American Journal of Physics 47, 482-487.
Brody, H. (1981) Physics of the tennis racket II: The sweet spot. American
Journal of Physics, 49, 816-819.
Brody, H. (1987) Tennis Science for Tennis Players, University of Pennsylvania
Press.
Brody, H. (1995) How would a physicist design a tennis racket?. Physics Today,
48, 26-31.
Howard Brody, Rod Cross and Crawford Lindsey, The
Physics and Technology of Tennis (available from www.racquettech.com)
Rod Cross and Crawford Lindsey, Technical Tennis (also available from www.racquettech.com)

Rod Cross, Crawford Lindsey and Howard Brody at the
TST2003 Tennis Conference organised by the International Tennis Federation in
London. A brief article about
Howard appears here.


