The solar wind is both super-Alfvenic and supersonic, with
Alfven Mach number 
and sonic Mach number
both typically 
. What happens when
the solar wind encounters an obstacle such as a planet's magnetic field,
atmosphere or solid surface? In each case the flow must be deflected around
the obstacle, either by Lorentz forces or by collisions (mediated by
electromagnetic forces). Information on the flow's
deflection, however, cannot reach the upstream plasma via the standard
(small amplitude) MHD waves - since the flow is super-Alfvenic and
supersonic. Accordingly the deflection must be accomplished by an MHD shock
wave.
Figure 13.1 illustrates the relevant plasma regions: the bow shock, which slows, compresses, heats and deflects the solar wind flow; the magnetosheath, in which the shocked solar wind is deflected further around the obstacle and eventually accelerated back up to the solar wind speed (downstream from Earth), eventually merging back into the solar wind where the shock weakens and disappears; the magnetopause, which separates the magnetospheric plasma from the shocked solar wind plasma; and the foreshock upstream of the shock but downstream of the tangent magnetic field lines.
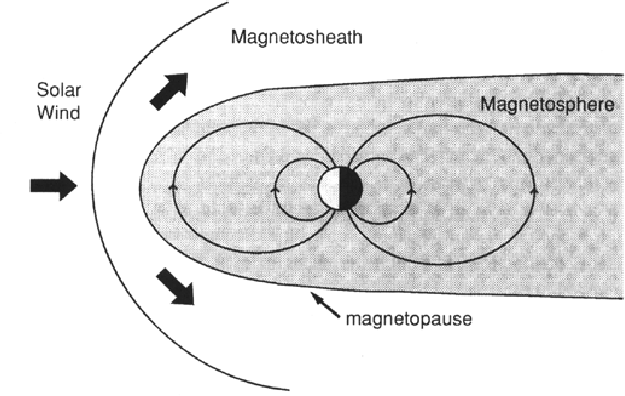
Figure 13.1: Schematic of Earth's bow shock, magnetosheath, and magnetopause [Cravens,
1997].
The characteristic shapes and boundaries are qualitatively familiar from the bow waves of ships, bullets, supersonic jets etc.
Qualitatively, a bow shock is just a nonlinearly steepened bow wave. An important aspect of this point is that the propagation speed of many wave modes depends on the wave amplitude (the MHD fast and slow modes and the whistler mode being examples); modes for which the propagation speed increases rapidly enough with wave amplitude can steepen nonlinearly (due to the intense parts of a wave packet piling up) and form shocks and other nonlinear structures such as solitons. One basic difference between solitons and shocks is that shock transitions depend intrinsically on dissipation and an increase in energy across the shock, contrary to the situation for solitons.
The position and shape of the bow shock depend on the ram pressure
Alfven and sonic Mach numbers, and the angle 
between the solar
wind velocity and magnetic field in the solar wind. This can be seen by
writing down the MHD equations in conservative form and then manipulating
them. In conservative form the MHD equations can be written:
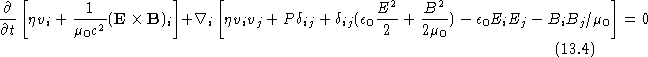
and
Normalising throughout by 
, 
, 
,
etc., in time-invariant systems these equations can be rewritten as
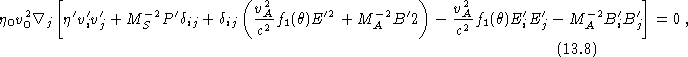
and
From Eqs (13.6) - (13.9) it can be seen that the overall ram pressure
becomes a scale factor for the system and that the
equations are otherwise only functions of 
, 
, 
, and the
angular variables. This is very important because it means that widely
applicable results can be obtained using an understanding built up from
a few calculations with different 
, 
, 
, and
angular variables.
The position and shape of Earth's bow shock, as well as the nature of
the shock transition, depend on , , , and the
angle between the upstream flow velocity and magnetic field
[e.g., Spreiter et al., 1966; Cairns and Lyon, 1995]. The overall
scale of the bow shock - magnetopause system is obtained by balancing
the solar wind ram pressure against the magnetic pressure of Earth's
dipole at the magnetopause, i.e.,
That is, the standoff distances for the magnetopause and bow shock (and by extension
their transverse scales) vary as 
. Thus, as expected from
intuition, higher ram pressures compress the magnetosphere and bring the bow shock
closer to Earth, while lower lead to the opposite effects.
The effects of variations in and are also relatively easy to see
qualitatively. For lower Mach number the wave speed is larger relative
to the flow speed, so that a wave will travel further upstream in a given
nonlinear steepening time, implying that the shock will be found further
upstream. Thus, for high the shock is closer to Earth and for low
it moves further from Earth. Changes in shock shape are also easy
to understand based on the concept of the Mach cone (Figure 13.2), which is the locus of
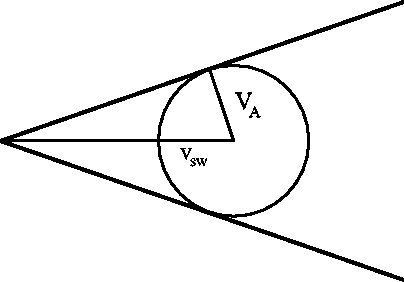
Figure 13.2: A disturbance moves out isotropically at 
but is carried downstream at 
. The tangent to the circle from
the initial point defines the Alfven Mach cone.
the maximum extent of a disturbance moving away from the obstacle at the wave speed. The Alfven Mach cone angle is given by
Thus, the shock shape becomes blunter for smaller and more
swept back for larger . This is consistent with simple intuition
for a slower and faster flow, respectively.
Figure 13.3 illustrates the changes in the shock's shape and location with
variations in .
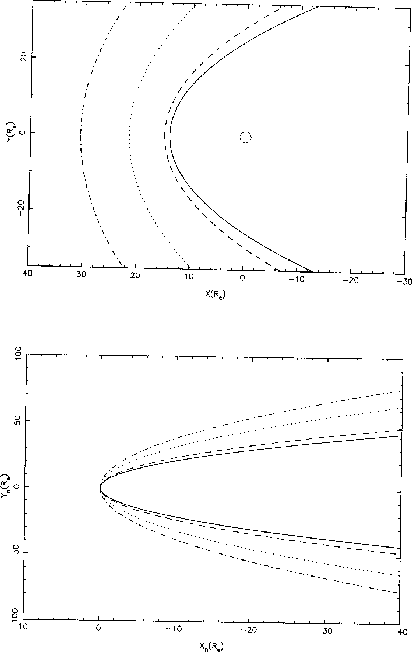
Figure 13.3: Changes in the shock's shape and location with variations in [unpublished
work by Cairns and Lyon, 1996]: 
(solid curves), 4.9 (dashed), 1.9 (dotted),
and 1.4 (fancy).
Note that the shock's nose moves sunward as decreases while the shock's
shape becomes increasingly blunt, as predicted from Eq. (13.11).
One implication of the solar wind's time-varying characteristics and
the dependence of the bow shock's location and shape on
, , and is that the bow shock is almost always
moving; it is a dynamic object. Times when it is almost stationary are
rare and therefore important for studies of the shock's intrinsic structure.