The magnetopause is the thin boundary separating the shocked solar
wind plasma from the plasma of the magnetosphere. Interior to the
magnetopause, in the magnetosphere, the plasma's motion is dominated by
Earth's magnetic field. The magnetopause has a thickness 
one thermal
(magnetosheath) ion gyroradius and it separates a high 
, low
magnetic field region (the magnetosheath) from the low , high
magnetic field region of the magnetosphere.
It can be questioned why the magnetopause exists at all: why is there a separation between the magnetosheath and magnetospheric plasmas? The basic reason is that both plasmas have high conductivities and the frozen-in approximations of MHD theory are well satisfied; the corollary of freezing-in one magnetic field is that all other magnetic fields are excluded from the plasma region, thereby requiring the existence of a plasma boundary separating the magnetosheath and magnetospheric plasmas.
Later it will become clear that the magnetopause does not completely separate the magnetosheath and magnetospheric plasmas. This is for several reasons. First, these plasmas are collisionless and non-MHD effects do exist and are important. An illustration of these points is that more energetic particles have larger gyroradii and so are able to traverse thin boundaries which do, however, separate the thermal particles of the two plasmas. Second, magnetic reconnection of solar wind and magnetospheric field lines is considered very important to space weather and the convection of plasma inside Earth's magnetosphere. This process allows solar wind plasma to enter and primarily populate Earth's magnetosphere but also allows plasma of terrestrial origin (especially ionospheric ions from the auroral regions and polar caps) to escape from the magnetosphere and enter the solar wind.
As described in Lecture 4, as well as shocks, there are two types of discontinuities in a collisionless MHD plasma: rotational and tangential discontinuities. Observationally the plasma density, pressure and vector magnetic field vary across the magnetopause, thereby requiring that the magnetopause be a tangential discontinuity. When the magnetopause is stationary it must be in equilibrium with all forces and torques balanced. Frequently this is described in terms of pressure balance, namely that
When the entire solar wind - shock - magnetopause - magnetosphere system is
in equilibrium, with the thermal pressure in the magnetosheath
( 
) equalling the solar wind ram pressure 
(i.e., neglecting the magnetic pressure there) then
It should be recalled (Lecture 3) that the equation of motion for a specific species of charged fluid is
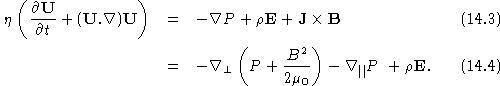
The question that should be answered at this stage is how thermal
pressure can physically play the role required by Eqs. (14.1) and (14.2) in
collisionless plasmas. Put another way, how can the (kinetic) motions of
individual particles in collisionless plasmas be reconciled with the role
inferred for the pressure in MHD and other fluid theories? It is shown next
that the required particle motions lead to currents that then lead to
forces that numerically have the magnitudes and
functional dependences of the thermal pressure of the plasma. The
magnetopause is considered specifically in this example but the results are
characteristic and widely applicable.
Consider a plasma attempting to move from an unmagnetized region into a region with a magnetic field (Figure 14.2):
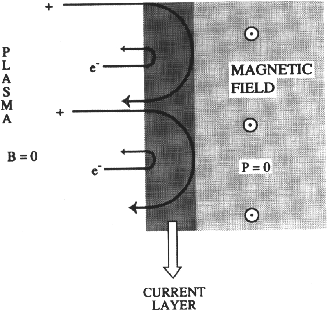
Figure 14.2: Schematic of the current layer which develops as a result of a thermal, unmagnetized
plasma (left) interacting with a magnetized region (right) [Cravens, 1997]. The electrons and
ions move on half a gyroorbit in the magnetized region, both species giving rise to a
downward current perpendicular to the magnetic field.
the thermal electrons and ions both execute approximately half
a gyro-orbit before finding themselves back in the unmagnetized region and with velocities
directed away from the magnetized region. This leads to the plasma being excluded from the
magnetized region. Moreover, notice that the current associated with this partial gyro-orbit
is in the same sense for thermal electrons and ions and that the
force has the direction required to push the plasma particles out of the magnetized region.
This analysis can be made quantitative. Defining the
initial direction of plasma motion as the 
direction, with the 
direction
up the page and the magnetic field in the 
direction, the total current for
thermal electrons and ions is
Notice next that the electron current layer is much narrower than the ion gyrolayer, with both having magnitudes of order a gyroradius thick. Integrating the total current over these layers leads to
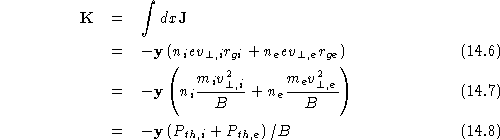
for a thermal (Maxwellian) plasma. Thus, integrated in over the current layer,
the integrated force 
.
Put another way, the 
force naturally balances the pressure force in the
fluid momentum conservation equation (3.32).
That is, the current in current layers separating kinetic,
collisionless plasmas with different properties naturally has the magnitude and direction
required for the resultant force to balance the tendency for
collisionless thermal plasmas to stream into regions with lower thermal pressure.
The above analysis can be generalized to the case where a cold plasma streams with uniform
velocity 
into a region with high magnetic field. In this case the thermal pressure in
Eq. (14.8) is replaced by the ram pressure 
. In the
case of both a directed motion and thermal motions it is intuitively clear that the effective
pressure which the current layer counteracts is the sum of the ram and thermal pressures. Showing
these results is left as an exercise to the reader.
These results on current layers explain why the concept of thermal pressure continues to have
relevance in collionless plasmas and also have numerous applications in the solar wind
(e.g., pressure-balanced structures) and magnetospheric physics. Of immediate relevance here is
the fact that it is the above force at the magnetopause current layer which
resists the motion of the magnetosheath plasma across the magnetopause, creates a magnetopause
obstacle, and which causes the bow shock to be located well away from the Earth.
The current layer also fulfills another purpose: confining the Earth's magnetic field to the region inside the magnetopause and the (weaker) magnetosheath field to the magnetosheath. Idealizing the magnetosheath to be unmagnetized, it is apparent that the idea of image currents is relevant: an image current flows on the magnetopause so as to remove the Earth's magnetic field from the magnetosheath but also to increase the field strength just inside the magnetopause. This can be seen in Figures 14.2 and 14.3.
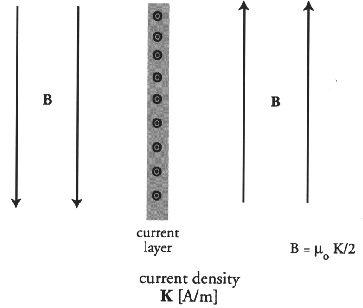
Figure 14.3: Schematic of the magnetic field produced by a current layer with line-integrated
current density K [Cravens, 1997].
Numerically, then the field just inside the magnetopause equals twice the field of the dipole at that distance; that is
Balancing the ram pressure of the solar wind against the force
and magnetic pressure of the Earth one then has
whence
or about 
for typical solar wind conditions (note: 
T is
the dipole magnetic field strength at the Earth's surface). This construction gives the
correct location for the magnetopause for normal solar wind conditions. Note that during times
of unusually large solar wind ram pressure the magnetopause may move substantially Earthwards.
Indeed, sometimes the magnetopause is observed inside geosynchronous orbit ( 
).
The magnetopause current layer is important in two other ways. First, the magnetic field associated
with the current layer is also observable at the surface of the Earth. This is particularly true during
times when the magnetopause is compressed Earthwards, leading to an increase in the magnetic field
measurable at the surface (since the current layer's field adds to the Earth's field inside the
magnetopause). As seen in Lecture 15, this effect can lead to an increase in the geomagnetic
activity index 
at the start of a geomagnetic substorm, while the subsequent increase of
the ring current leads to major decrease of the surface field (Section 14.3).
Second, and perhaps more importantly, the magnetopause current layer is a global phenomenon that persists wherever the magnetopause does. How does this global current system close? This is one of the questions pursued in the rest of this lecture and the next two lectures. Figure 14.4 gives a first view of the global nature of the magnetopause current system and the way in which the current loops close.
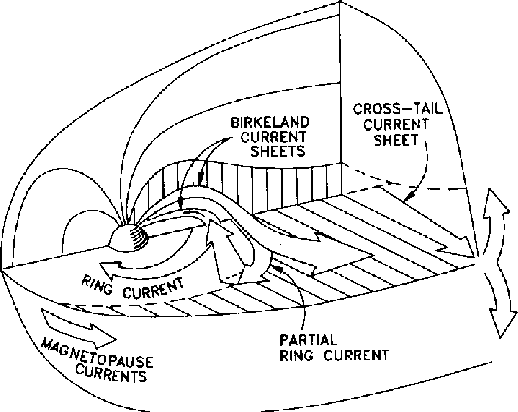
Figure 14.4: The main current systems flowing in Earth's magnetosphere [Stern, 1994],
showing the magnetopause current system, ring current, and the cross-tail current. .
Consistent with Figures 14.2 and 14.3 the magnetopause current is primarily westward near the equator at the front and mid-tail regions of the magnetopause, before turning above/below the magnetic equator (more properly, the tail's current sheet) and closing on the eastward side of the magnetopause. Figure 14.5 shows that the magnetopause currents change direction near the polar cusps discussed more below, flowing primarily eastwards sunwards of the cusps.
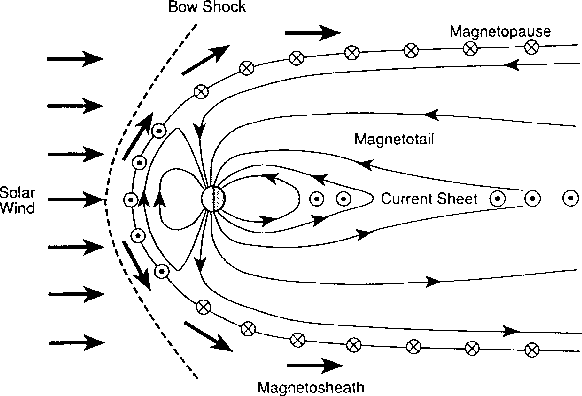
Figure 14.5: Cross section of the global magnetosphere, showing the magnetopause current system, the
cusps, the magnetotail, and the magnetotail current sheet [Hughes, 1995].
The final topic discussed now and in Lecture 15 is that of magnetic reconnection at the magnetopause. Suppose that the solar wind magnetic field in Figures 14.4 and 14.5 is directed southwards. Since the dipole field lines are directed northwards this situation involves anti-parallel magnetic field lines being brought together by a plasma flow, thereby suggesting that magnetic reconnection might occur. Magnetic reconnection can lead to magnetosheath and solar wind plasma entering the magnetosphere and magnetospheric plasma escaping into the magnetosheath and solar wind, as well as the creation of accelerated and heated plasma flows and modified magnetic topologies. All these effects are observed. It is perhaps less obvious, but magnetic reconnection is believed to occur sometimes even during times of northward IMF direction and to sometimes involve the east-west components of the magnetic field. These reconnection events occur away from the nose of the magnetopause.