Photoionization reactions can be written
where M represents an atom or molecule. The only requirement is that the photon energy h 
exceed the
relevant ionization potential 
. Since typically exceeds 10 - 20 eV, this means that
only radiation with 
nm can cause photoionization. Any excess photon energy appears
primarily as kinetic energy for the escaping photoelectron. Photoelectron energies can thus range from
zero to hundreds of eV.
Consider a plane-parallel atmosphere which has a certain photon flux at wavelength 
incident
at the top. Photoionization causes the photon flux to decrease (and the number of photoelectrons and
ions produced to increase) along the path. The flux at altitude z is given by
where 
is the optical depth given by
is the neutral density, and 
is the photon-absorption cross section.
Figure 16.5 shows that 
is the angle between the line-of-sight path and the
zenith direction.
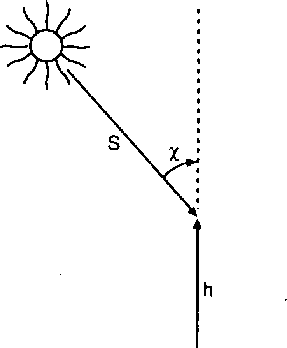
Figure 16.5: Geometry of the ray path, showing the zenith angle and the height z (or h)
[Luhmann, 1995].
Assuming that is an exponential function, as in Eq. (16.5), then
the integral can be performed to yield
where 
is the scale height for neutrals.
This equation can be used to model the source of ionization as a function of altitude,
the degree of absorption of the radiation, and changes in the ionosphere with time-of-day
(through the zenith angle dependence). Pursuing this last point, as increases,
the altitude for a given 
increases, so that the total ionization rate decreases
(since 
is lower then). This implies considerable variations in the locations and
amounts of ionization produced as a function of time during the day. These daily motions and
variations in the ionosphere, when considered in conjunction with recombination and other loss
processes, give rise to changes in the magnetic field observed on the
ground, the so-called diurnal variations that must be substracted when attempting to
quantify space weather effects.