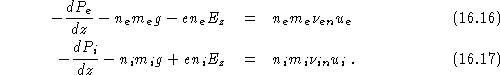
Consider just one ion species, one neutral species and electrons. Furthermore, consider only the vertical structure and vertical motions, neglect the magnetic field, and assume that the neutrals are stationary, that the ions and electrons have identical vertical velocities in the time-steady state, and that a time-steady state exists. Then all the ion-electron coupling terms cancel out below and the d/d t terms are zero. The electron and ion momentum equations are then
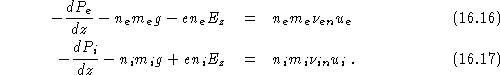
Rewriting these equations in terms of 
and then adding them yields
for 
.
Solving then for 
then yields
Note that in the special case of an isothermal ionosphere ( 
), then 
to a high
degree of accuracy. Another point is that plasma flows are typically present. In this one-species case,
the flow corresponds to outflow of the ionospheric plasma. As discussed more below, this physics is the basis for
``exospheric'' models for the polar wind out of Earth's ionosphere and for the solar wind.
Before proceeding, let us just note that this system of equations resembles a diffusion equation.
Assuming that 
and 
are constant, then the last equation above can be rewritten
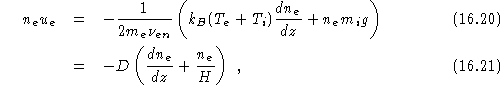
where H is the usual scale height and 
. Combining this final form with the
number conservation equation it can be shown that a diffusion equation results:
Thus, both electrons and ions can diffuse in altitude, so that the peak plasma density need not be where the peak ionization is.