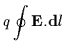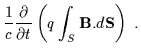Next: Magnetic Mirrors: the effects
Up: Single Particle Motions: ``Orbit
Previous: Applications
For periodic motions the theory of mechanics shows that quantities called actions can remain invariant
for slow changes in the system. An action J can be defined in terms of generalized coordinates
qgen and conjugate momenta pgen by
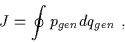 |
(2.31) |
where the integral is over one period of the motion. A particle's gyromotion is one example of a
periodic motion amenable to the construction of an approximate constant of the motion (or invariant).
Defining qgen to be the gyrophase 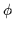 ,
then the angular momentum
,
then the angular momentum
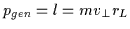 is the conjugate momentum. Inserting these variables into (2.31) and integrating one finds
is the conjugate momentum. Inserting these variables into (2.31) and integrating one finds
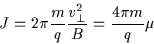 |
(2.32) |
for slowly varying B. The quantity
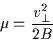 |
(2.33) |
is known as the first adiabatic invariant of a plasma particle. This implies that a
particle's perpendicular energy
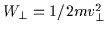 is proportional to
B if
is proportional to
B if 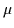 is constant.
is constant.
Another, perhaps more obvious derivation of the first adiabatic invariant
is as follows. Assume that the particle sees a small change in 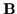 during a
gyroperiod, whether due to temporal or spatial variations in
during a
gyroperiod, whether due to temporal or spatial variations in 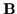 .
I.E.,
.
I.E.,
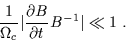 |
(2.34) |
The change in 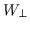 in one gyroperiod is
in one gyroperiod is
Assuming the orbit size changes very little in one gyroperiod then
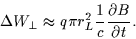 |
(2.37) |
Since the change in B in one gyroperiod is
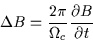 |
(2.38) |
then
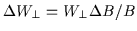 or
or
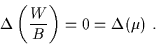 |
(2.39) |
That is, 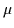 is a constant.
is a constant.
Other adiabatic invariants also exist. The second or longitudinal
adiabatic invariant is associated with the periodic bouncing of particles in
magnetic flux tubes and magnetic bottles:
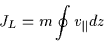 |
(2.40) |
A third adiabatic invariant can be associated with the periodic drift of a particle
(due to 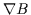 and curvature drifts) around a dipole magnetic field. It is
useful for studying particle motions in Earth's magnetosphere but is not
addressed further here.
and curvature drifts) around a dipole magnetic field. It is
useful for studying particle motions in Earth's magnetosphere but is not
addressed further here.



Next: Magnetic Mirrors: the effects
Up: Single Particle Motions: ``Orbit
Previous: Applications
Iver Cairns
1999-08-04
![]() during a
gyroperiod, whether due to temporal or spatial variations in
during a
gyroperiod, whether due to temporal or spatial variations in ![]() .
I.E.,
.
I.E.,