BAT AND BALL COLLISIONS

The following discussion describes the collision between a bat or racquet or club and a ball, in terms of the basic physics. A more complete discussion can be found in my Physics of Baseball and Softball book or in our Physics and Technology of Tennis book.

Here are 4 diagrams showing how a force F can act on a mass M. The mass is drawn as a rectangular block, but it can have any shape at all. M can represent a bat or racquet or a block of wood. When struck by a ball, the force F acts only for a short time, and it changes with time. Since F = M dV/dt, or F dt = M dV, the impulse (force x time) = change in momentum.

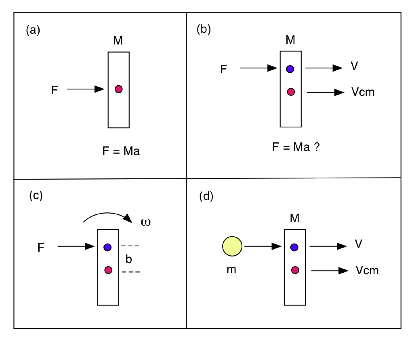
In (a), F acts in line with the centre of mass, shown as a red dot. In that case, M accelerates according to the relation F = Ma or a = F/m. All parts of the mass accelerate at the same rate, and all parts of the mass move to the right with velocity V = at, where t is time, assuming that M was at rest at the start.

In (b), F is applied near one end of M, in line with the blue dot. In that case, what happens to our F = Ma formula ? We can still use F = Ma, but a is the acceleration of the red dot (the centre of mass) rather than the acceleration of the blue dot. As a result, Vcm = at, as it was in (a). The blue dot accelerates faster than the red dot, because the whole mass rotates, as shown in (c)

In (c), the force is applied in line with the blue dot, located a distance b from the red dot. As a result, there is a torque = Fb acting about the centre of mass, and M rotates at angular velocity w. If I = moment of inertia of the mass, for rotation about an axis through the centre of mass, then Fb = I dw/dt

Given that the centre of mass translates at velocity Vcm, and the blue dot rotates at speed bw around the red dot, the speed of the blue dot is V = Vcm + bw, at least for a short time - before the whole mass has rotated through a large angle. In that case, the acceleration of the blue dot is dV/dt and we can write

F = Me dV/dt

where Me is the effective mass of the blue dot. We can derive a formula for Me by noting that

F = Me (dVcm/dt + b dw/dt ) = Me (F/M + Fb²/I)

so 1/Me = 1/M + b²/I

Note that if b = 0 then Me = M, otherwise Me is less than M.

In (d), a ball impacts the mass M in line with the blue dot and exerts a force F on the mass. If the mass of the ball is less than Me, then the ball will bounce backwards. The ball bounces best if it bounces in line with the red dot, since then Me = M. Whenever there is a collision like this, there is a decrease in the total kinetic energy due to energy losses in the ball and vibrations of the mass M. The reduction can be measured in terms of the rebound speed of the ball. The ratio of the rebound speed to the incident speed, when the mass M is initially at rest, is called the apparent coefficient of restitution, eA. Measurements of eA at various impact points completely specify the performance of a bat or racquet, at least in terms of the outgoing ball speed. The outgoing ball spin is a separate issue. The maximum speed at which the bat can be swung is also a separate issue, and it depends on the swing weight of the bat, as well as the strength of the person swinging it.

___________________________________________________________________________