Physics of Cricket

Copyright © 2005. The following articles cannot be reproduced in any format without permission.

In Australia, as in other parts of the British Empire, boys (such as myself here) learn to play cricket at a relatively young age. Cricket is a subtle game requiring a great amount of patience as well as skill. It takes 5 days to complete a Test match so the grass needs to be mown and the pitch needs to be rolled as the game progresses. It is not something that is easy to learn and appreciate as an adult, especially by North Americans.

1. Heavy vs Light Bats

The crowd loves a batter who can hit sixes. If you want to hit the ball as fast and far as possible, should you use a light or heavy bat? That's an age old question with plenty of answers, but which is the correct answer? Light bats can be swung faster than heavy bats, but only about 10% faster (for the usual range of bat weights). Imagine hypothetically that the bat weighs 10 grams - light as a feather. If you swing it as fast as possible, you might get the tip to travel at say 160 km/hr. Now double the weight to 20 gm. This time the tip travels at about 159 km/hr. The problem here is that your arms weigh about 8 kg all up, so the extra 0.01 kg is hardly noticeable. Most of the effort needed to swing a bat goes into swinging the arms. That's why light bats can be swung only about 10% faster than heavy bats.

If a light bat was swung at the same speed as a heavy bat and both hit the same ball, the heavy bat would pack more power since it has more energy and more momentum. But light bats can be swung 10% faster. If a bat is swung 10% faster, the ball comes off the bat about 7.5% faster. That almost makes up for the fact that light bats are basically less powerful when swung at the same speed as heavy bats. The end result is that heavy bats are about 1% more powerful than light bats. Having a heavy bat is a definite advantage if you swing all bats at the same medium speed, but if you need to move the bat quickly into position to strike the ball, a light bat will get there faster. Heavy for a 10 year old might be light for a 100 kg cricketer, so the real answer for raw bat power is to use a bat that is as heavy as feels comfortable to swing.

2. The Sweet Spot

Every batter knows that there is a special spot on a bat where the shot feels best. It sometimes feels so good that there is almost no sensation at all that the bat hit the ball. It's the same with a baseball bat or a tennis racquet or a golf club, so there is nothing special in this respect about cricket bats. Two special points on a bat are good candidates for the sweet spot. Technically, they are known as the fundamental vibration node and the centre of percussion. The node point is concerned with bat vibrations. Most impact points on a bat will cause the whole bat to vibrate, including the handle. Those vibrations persist well after the ball has left the bat, and they tell you whether you hit the ball cleanly. The biggest vibrations result when the ball strikes the tip of the bat. However, there is a spot about 150 mm from the tip where an impact causes no vibrations at all. That is the node point. As the impact point moves closer to the node point, bat vibrations get weaker and the shot feels nicer.

An impact near the tip of a bat will generate bad vibrations and it will also cause the handle to jerk forwards (towards the bowler), pulling your hand and arm with it. An impact higher up, near the handle, will push the handle backwards towards the body. In both cases there is a certain amount of jarring that feels unpleasant. The result is a sudden shock to the arm in one direction rather than a back and forth vibration. There is an impact point between the tip and the handle where there is no sudden motion of the handle at all. That point is called the centre of percussion. However, recent measurements show that it is too close to the handle to qualify as the sweet spot that batters talk about.

3. Vertical bounce of a cricket ball

Almost every type of ball used in a sporting event must bounce according to the rules of the game. If the ball bounces too high or too low, the players will complain that something is wrong with it. The standard test for bounce is to drop a ball from a certain height onto a hard surface such as a slab of concrete and then measure how high it bounces. When a tennis ball is dropped from a height of 100 inches (2.54 m) it must bounce to a height between 53 inches (1.35 m) and 58 inches (1.47 m). For official use in major tournaments, tennis balls must be properly tested and approved, for a moderately large fee, but the fee is only a small fraction of the total value of balls sold. Tennis courts themselves vary in hardness, which affects bounce height, so a standard surface such as concrete is used for these tests.

There is no such official rule for a cricket ball. There is simply a tradition that is monitored by umpires, and one that is an industry standard. When a cricket ball is dropped from a height of 2.0 m onto a heavy steel plate, it bounces to a height somewhere between 0.56 m and 0.76 m. Cricket balls are a lot less bouncy that tennis balls and the permitted range of possible bounce heights is larger. A useful way of specifying the bounce is to take the ratio of the bounce speed to the incident speed. When a ball is dropped from a height of 2.0 m it lands at a speed of 6.26 m/s, regardless of the type or weight of the ball. A cricket ball bounces to about one third of that height (0.67 m), in which case it rebounds at a speed of 3.61 m/s. The ratio of these two speeds is 3.61/6.26 = 0.58 and is called the coefficient of restitution (COR). The COR of a tennis ball is about 0.75. The COR determines not only the bounce height but also the speed at which a ball comes off the bat. The batted ball speed also depends on the speed of the bat.

4. Batted ball speed

Suppose that a cricket ball is bowled at 100 km/hr, the batter swings the bat at 60 km/hr, and hits the ball straight back over the bowler's head. How fast does the ball come off the bat? This is a simple question but the answer is not so simple since it depends on which part of the bat is moving at 60 km/hr and it depends on where the ball makes contact with the bat. Suppose that the ball strikes the middle of the bat rather than near an edge and suppose that 60 km/hr is the speed of the impact point on the bat rather than the speed of the tip or the handle. We also need to know the mass of the bat, or better still we need to know how fast the ball comes off the bat when the bat is not swung at all. Suppose that the bat is used just to block the ball and the ball bounces off the bat at 20 km/hr. If E = ratio of bounce speed to incident speed = 20/100 = 0.2 then the speed of the ball when the bat is swung at speed V is 20 + (1 + E)V = 20 + 1.2 x 60 = 20 + 72 = 92 km/hr. For most bats, E varies from about 0.1 near the tip to about 0.3 half way up the bat. E is smallest near the tip of the bat but V is biggest there when the batter takes a huge swing at the ball.

5. Grip firmness

The effectiveness or the power of any given bat can be tested without swinging the bat at all. If the bat is held in a fixed position and a ball is fired at the bat at say 100 km/hr, the ball will bounce off the bat at a speed of about 20 km/hr. That speed gets added to the bat speed when the bat is swung. A surprising result is that the bounce speed off a fixed bat does not depend on how firmly the handle is held. It can be gripped in a vice or it can be dangled on the end of a piece of string and the ball will bounce at exactly the same speed. For that reason, the speed of a struck ball does not depend on how firmly the handle is gripped in the hands.

There is a simple reason for this strange result. When the ball strikes the bat, it causes the bat to bend slightly at the impact point. That bend then propagates along the bat up to the handle, reflects off the end of the handle and then travels back down to the impact point. The bend takes about 0.002 seconds to travel up to the handle and back again. But the ball is on the bat for only 0.001 seconds, and it bounces off before the reflection gets back to the impact point. The ball has no way of knowing how the handle was held so it bounces off the bat at the same speed regardless of how the handle is gripped. The handle could be attached by a hinge and the ball would still come off the bat at the same speed.

6. Force on a cricket ball

Drop a cricket ball on a cricket pitch and the ball bounces up off the pitch. How long does the ball remain in contact with the pitch and how big is the force on the ball? Cricket balls are relatively stiff compared to say a tennis ball, and the contact time is shorter. A tennis ball spends 0.005 seconds in contact with the court or the strings of a racquet. A cricket ball spends about 0.001 seconds in contact with the pitch or in contact with a bat. The force on the ball has to slow it down to a complete stop and then accelerate it back in the other direction, all in the space of 0.001 seconds. Suppose that a 0.16 kg cricket ball hits a bat at 100 km/hr and then comes off the bat at 100 km/hr in the reverse direction. Imagine a car accelerating from 0 to 100 km/hr in 0.001 seconds. That's a lot of acceleration. A Porshe can do it in 5 seconds, but a cricket ball does it 10,000 times faster. The average force on the ball is 8,800 N, enough to lift a mass of 880 kg off the ground. The peak force on the ball is about double that, enough to lift a 1.76 tonne car off the ground. That's why it hurts to get struck on the head or anywhere else with a cricket ball.

7. Air resistance

Air plays an important role in cricket. Apart from allowing players to breathe, it causes the ball slow down through the air and it can cause a ball to curve or swing away from the path it would otherwise follow. Air is heavier than you might expect. One cubic metre of air at ground level weighs 1210 gm. A cricket ball weighs 160 gm. A room full of air weighs more than most cricket players.

If you drop a cricket ball out of a helicopter hovering 300 m above the ground, it will accelerate up to 123 km/hr in about 5 seconds, having fallen through a distance of about 100 m. It will then fall the remaining 200 m to the ground at 123 km/hr, without gaining any additional speed. At 123 km/hr, the force of gravity pulling the ball down is equal to the drag force of the air pushing it upwards. The total force on the cricket ball is then zero so it falls at constant speed after the first 100 m. A more dramatic effect would be seen if you dropped a cricket ball into a swimming pool. Air has the same basic effect as water in slowing the ball, but it is a smaller effect.

A ball bowled horizontally at 123 km/hr experiences a backwards horizontal drag force that is equal to the weight of the ball. At world record bowling speeds around 160 km/hr, the drag force is 1.7 times greater than the weight of the ball. Regardless of the speed of the ball when it leaves the bowler's hand, air resistance causes the ball to slow down by about 12% by the time it lands on the pitch. It slows down by another 30% or 40% when it hits the pitch, depending on the speed of the pitch and the angle of incidence. A ball bowled at 150 km/hr will arrive 0.46 s later at the batter's end, travelling at about 85 km/hr.

8. Collision between bat and ball

What happens to a ball when it hits a bat? It comes in at around 100 km/hr, reverses direction, and bounces off the bat 0.001 seconds later. But what happens during that 0.001 second it is on the bat? Assuming that the ball is hit in the middle of the bat and heads off straight back to the bowler, all that happens is that the ball squashes, comes to a complete stop, expands back to its original shape and then leaves the bat. If the ball comes off at some other angle, then it hits the bat at an angle and starts to slide across the bat. As it does so, it slows down in a direction perpendicular to the face of the bat and it slows down in a direction across the bat. In addition it will start to rotate if it had no rotation to start with, otherwise the rate of rotation will either decrease or increase depending on the original direction of rotation. The part of the ball in contact with the bat will then grip the bat without any further sliding or rolling, while the rest of the ball continues to rotate. The ball therefore gets twisted out of shape as well as getting severely squashed. As the ball starts to come off the bat it expands back towards its original shape, it releases its grip on the bat, there is a sudden change in the rate of rotation, and the ball slides backwards off the bat. Most likely, the ball will come off the bat spinning much faster than it was before it hit the bat.

9. Wicket keeping

Suppose that a wicket keeper needs to move as fast as possible to the right to catch a ball. Which foot should move first, and in what direction? It seems obvious that his left foot should stay on the ground and his right foot should move to the right while pushing as hard as possible to the left with the left foot. That way, his whole body and every part of it moves rapidly to the right. But suppose he pushes to the left with his left foot and moves his right foot to the left. That way, he will tend to fall over to the right and his upper body moves even faster to the right. Such a step is called a gravity-step and it is counter-intuitive.

The same situation arises when a tennis player is facing a 200 km/hr serve and needs to move as fast as possible to the right. High speed film shows that players who move their right foot to the left, before moving it to the right, get their racquet to the ball faster. The physics explanation is that keeping the feet together reduces the moment of inertia and the upper body will therefore rotate faster. The same sort of thing happens when a diver wants to do a double or triple somersault. Tucking the arms and legs in reduces the moment of inertia and the diver spins faster.

10. World's fastest bowler

The cricket equivalent of a 4 minute mile is to bowl a ball at 100 mph (161 km/hr). Akhtar and Lee have come close, but noone knows for sure if they have actually done it yet. The newspapers said that Akhtar did it in 2002, but how do we know that the radar gun was correct? I know for a fact that it wasn't correct because they never are. That's because (a) the ball doesn't travel straight at the gun and (b) the ball slows down down through the air by 0.6 mph after it travels the first 1.0 m. If a 100 mph ball travels 5 degrees away from the gun the speed will be recorded as 99.6 mph. Balls are bowled about 5 degrees down from the horizontal and anything up to 5 degrees horizontally away from the middle stump. That can give an error of around 1 mph in the recorded speed.

In order to get the speed to the nearest 0.1 mph, the gun would need to point almost exactly in line with the ball and it would need to capture the speed before the ball travels 160 mm out of the bowler's hand. That means the gun has to be located near the stumps. Also, the ball can't rotate because it might gain an extra 1 mm if the seam comes into view, so it could gain an extra 0.6 mph.

If someone ever bowls a ball at 101 mph then there will be a good chance that it was actually 100 mph or more. Until then Akhtar's 161 km/h (100.04 mph) should be taken with a grain of salt. All recorded speeds should be quoted as plus or minus 1 mph or whatever the appropriate margin of error happens to be.

11. Ball spin

Spin bowlers have lots of tricks up their sleeve since a ball can be spun in many different ways. A cricket ball, like anything else, has three main axes about which it can spin. Each spin axis has a different effect on the flight of the ball through the air and a different effect on the way the ball bounces. The three axes are perpendicular to each other. The first axis is vertical, pointing to the sky, and the other two are horizontal. The second axis points along the pitch towards the batter. The third axis points across the pitch. A ball can also be spun about an axis that is inclined at an angle to the three main ones, in which case it will have a component of spin about each of the main axes.

A ball that spins about a vertical axis will swerve to the left or right through the air (like a golfer's hook or slice shot) depending on the spin direction. There is no kick when it bounces since there is no preferred direction in which it can kick.

A ball that spins about the second axis does not swerve at all through the air. However it will kick sharply to the left or right when it bounces, depending on the amount and direction of spin. The ball kicks in the same direction of motion as the top of the ball. Drop a spinning ball vertically onto the pitch and you will see why.

Topspin or backspin results when the ball spins about the third axis. A topspin ball dives down towards the pitch faster than a ball without spin, and it bounces at a reduced angle since it kicks forwards when it bounces. A backspin ball tends to float through the air and kicks up when it bounces since it tends to kick backwards, causing the ball to slow down more than a ball without spin. The actual result depends on both the amount of spin and the angle of incidence. If a non-spinning ball is incident at an angle of about 20 degrees to the horizontal, then it will slide along the pitch until it bounces,  at about 22 degrees to the horizontal. If the ball has backspin then the trajectory will probably be different. It depends on the ball speed and launch angle or on where the ball lands. In general,  a ball with backspin landing at the same spot will be incident at a lower angle, say 18 degrees, and it will bounce up at about 20 degrees. But if the bowler sends down a slower backspin ball and if it lands at an angle of incidence of say 40 degrees, then the ball will start to slide along the pitch for a while and then grip the pitch before it bounces. This will cause the ball to slow down a lot during the bounce, so it will bounce up quite steeply, say at 50 degrees. The formula for the bounce angle is:

Slope of bounce angle = (vertical bounce speed) / (horizontal bounce speed)

where slope means the same thing as tangent in trigonometry. So, the effect of backspin or topspin depends on whether the ball slides throughout the bounce (as it does at low incident angles) or whether it gets a chance to grip the pitch, as it does at high angles of incidence.

12. Swing bowling

A cricket ball can swerve to the left or the right as it moves through the air, either because it spins about a vertical axis or because it spins about an axis perpendicular to the seam. Vertical axis spin is commonly used by spin bowlers by not by fast bowlers. Fast bowlers prefer to swing the ball by making sure the seam is inclined at an angle of about 20 degrees to the direction that the ball is headed, in such a way that about 3/4 of the front of the ball is smooth. That way, the air flows smoothly around the smooth half but it becomes turbulent on the other side since it has to flow past the seam. Turbulent air is at a lower pressure than smooth flowing air, so the ball gets pushed sideways. It is almost impossible to eliminate backspin as the ball leaves the bowler's hand, but if the spin axis is perpendicular to the seam then it will help to keep the seam aligned at a fixed angle.

The sideways force on the ball peaks at about 110 km/hr, drops to zero at about 120 km/hr and then reverses direction. Reverse swing arises because the air flow on the smooth side becomes turbulent at sufficiently high ball speeds. The smooth side then becomes the low pressure side so the ball swings in the opposite direction. Normally, this effect is significant only at speeds above about 140 km/hr. However, the effect can occur at lower speeds if the ball has a roughened side and if the roughened side faces forward. Conventional swing bowlers polish the ball so one side is as smooth as possible. Reverse swingers like to make sure the other side is as rough as possible. The best ball to swing is therefore one that stays smooth on one side and roughens up during normal play on the other side.

Details of the aerodynamics involved are described on my home page under the heading Ball Trajectories where you can find several pdf files to download on the subject, including one called Sports Balls.pdf and one called Fluidflow Photos.pdf. The secret behind swing bowling lies in the way that the thin boundary layer of air near the ball surface can separate from the ball either early or late depending on whether the air flows smoothly over the surface or is tripped into turbulence by the seam or by roughness of the surface, or both. 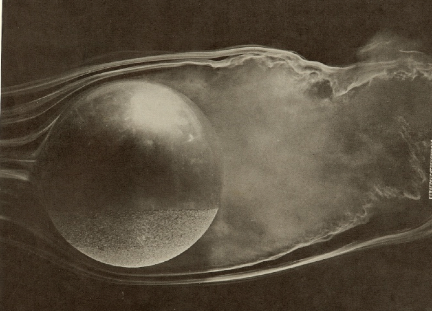Those boundary layers were revealed many years ago by the marvelous smoke tunnel photos shown in the Photos.pdf file. Here is one taken by the late Professor F. Brown from University of Notre Dame showing how air flows around a sphere when part of the bottom half is covered in a rough grit. Air separates early over the smooth portion, becomes turbulent over the rough portion and separates later, so the air is deflected upward, resulting in an equal and opposite downward force on the ball. That is the secret that lies behind almost all aerodynamic flows, and it is what determines both the lift and drag coefficients acting on an object. Note how air backflows into the low pressure “hole” left behind the ball, forming a turbulent wake. This photo is protected by copyright.