


Next: Curvature drifts
Up: Motion in non-uniform magnetic
Previous: Motion in non-uniform magnetic
Figure 2.3 shows the path of a positively charged particle in this case. Assuming
that the gradient is on scale lengths long compared with the gyroradius, i.e.,
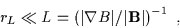 |
(2.17) |
the orbit
is almost circular but does not quite close. Since
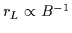 ,
rL
will be slightly smaller where B is larger and slightly larger where B is smaller.
This causes the orbit to drift in the direction of its gyromotion where rL is
larger, perpendicular to both
,
rL
will be slightly smaller where B is larger and slightly larger where B is smaller.
This causes the orbit to drift in the direction of its gyromotion where rL is
larger, perpendicular to both 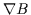 and to
and to 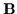 .
A negatively charged
particle drifts in the opposite direction. The physics is thus clear.
.
A negatively charged
particle drifts in the opposite direction. The physics is thus clear.
Quantitatively we write
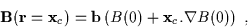 |
(2.18) |
where
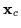 represents the unperturbed gyromotion and
represents the unperturbed gyromotion and 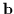 is the unit vector
of the magnetic field. The perpendicular equation
of motion is
is the unit vector
of the magnetic field. The perpendicular equation
of motion is
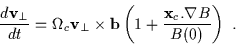 |
(2.19) |
The particle velocity is now written as
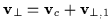 ,
where
,
where
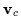 represents the unperturbed gyromotion and
represents the unperturbed gyromotion and
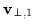 is the sum of the drift
velocity and any first order perturbations to the gyromotion. Substituting into (2.19),
grouping the zeroth order terms and deleting them, and
ignoring the second order term
is the sum of the drift
velocity and any first order perturbations to the gyromotion. Substituting into (2.19),
grouping the zeroth order terms and deleting them, and
ignoring the second order term
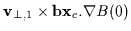 ,
the
first order equation becomes
,
the
first order equation becomes
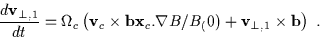 |
(2.20) |
This equation is next averaged over a gyroperiod and
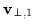 is identified as the
constant drift velocity
is identified as the
constant drift velocity
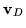 ,
so that the time derivative becomes zero and the drift
velocity obeys the equation
,
so that the time derivative becomes zero and the drift
velocity obeys the equation
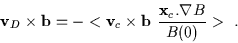 |
(2.21) |
Now
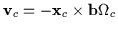 and the time-average
of the righthand term simplifies considerably since the x component of the
term
and the time-average
of the righthand term simplifies considerably since the x component of the
term
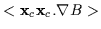 becomes
becomes
with a similar result for the y component. That is,
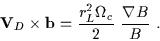 |
(2.24) |
Rearranging, the final result is
The 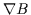 drift speed therefore depends on the charge, mass, and perpendicular energy of the
particle, as well as on the magnetic field strength and the scale length of the gradient. This
drift can therefore cause currents and charge separations in the plasma. Moreover, as seen below,
the combination of a convection electric field and a
drift speed therefore depends on the charge, mass, and perpendicular energy of the
particle, as well as on the magnetic field strength and the scale length of the gradient. This
drift can therefore cause currents and charge separations in the plasma. Moreover, as seen below,
the combination of a convection electric field and a 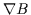 plasma drift can lead to particle
acceleration.
plasma drift can lead to particle
acceleration.



Next: Curvature drifts
Up: Motion in non-uniform magnetic
Previous: Motion in non-uniform magnetic
Iver Cairns
1999-08-04
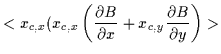
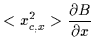
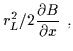
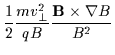
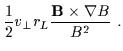
![]() drift speed therefore depends on the charge, mass, and perpendicular energy of the
particle, as well as on the magnetic field strength and the scale length of the gradient. This
drift can therefore cause currents and charge separations in the plasma. Moreover, as seen below,
the combination of a convection electric field and a
drift speed therefore depends on the charge, mass, and perpendicular energy of the
particle, as well as on the magnetic field strength and the scale length of the gradient. This
drift can therefore cause currents and charge separations in the plasma. Moreover, as seen below,
the combination of a convection electric field and a ![]() plasma drift can lead to particle
acceleration.
plasma drift can lead to particle
acceleration.