Distribution functions

The particle distribution function 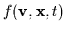$f({\bf v},{\bf x},t)$ is defined so that the total number of particles in a differential six-dimensional phase space element 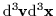${\rm d}^{3}{\bf v} {\rm d}^{3}{\bf x}$ is equal to 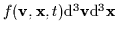$f({\bf v},{\bf x},t) {\rm d}^{3}{\bf v} {\rm d}^{3}{\bf x}$. The particle number density (number of particles per unit volume) is

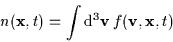$$n ({\bf x},t) = \int {\rm d}^{3}{\bf v} \, f({\bf v},{\bf x}, t)$$ (3.1)

Other physical quantities are obtained by taking moments, where the moment of quantity 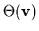$\Theta ({\bf v})$ is defined by

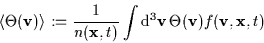$$\langle \Theta ({\bf v}) \rangle := \frac{1}{n ({\bf x},t)} \int {\rm d}^{3}{\bf v} \, \Theta ({\bf v}) f({\bf v},{\bf x}, t)$$ (3.2)

Using (3.2), the following physical quantities are defined for particle species 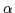$\alpha$:

• Fluid velocity:
  

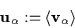  $${\bf u}_{\alpha} := \langle {\bf v}_{\alpha} \rangle$$ (3.3)

  
  

• Mean thermal velocity:
  

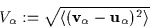  $$V_{\alpha} := \sqrt{\langle ({\bf v}_{\alpha}- {\bf u}_{\alpha})^{2}\rangle}$$ (3.4)

  
  

• Mass density:
  

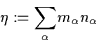  $$\eta := {\displaystyle \sum_{\alpha}} m_{\alpha} n_{\alpha}$$ (3.5)

  
  

• Mean mass velocity:
  

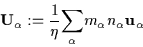  $${\bf U}_{\alpha} := \frac{1}{\eta} {\displaystyle \sum_{\alpha}} m_{\alpha} n_{\alpha} {\bf u}_{\alpha}$$ (3.6)

  
  

• Velocity of particle relative to mean mass velocity:
  

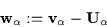  $${\bf w}_{\alpha} := {\bf v}_{\alpha} - {\bf U}_{\alpha}$$ (3.7)

  
  

  
  

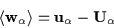  $$\langle {\bf w}_{\alpha} \rangle = {\bf u}_{\alpha} - {\bf U}_{\alpha}$$ (3.8)

  
  

• The pressure tensor 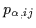$p_{\alpha,ij}$ is defined in terms of $w_{\alpha,i}$:
  

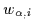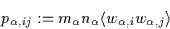  $$p_{\alpha,ij} := m_{\alpha} n_{\alpha} \langle w_{\alpha,i} w_{\alpha,j} \rangle$$ (3.9)

  
  

The equilibrium velocity distribution function is a Maxwellian, with

$$f({\bf v})=\frac{n}{(2 \pi)^{3/2} m^{3} V^{3}} {\rm exp}\left[ \frac{-v^{2}}{2 V^{2}} \right] \, .$$ (3.10)

Other distributions are often detected in space plasmas; for example, bi-Maxwellians with different temperatures in directions parallel and perpendicular to the background magnetic field, and generalized Lorentzian (or Kappa) distributions which depart from the Maxwellian functional form at high energies and obey a power law.