BILLIARDS

1. Billiard Ball Collisions

MovieA shows a typical head-on collision between two billiard balls when one is initially at rest. Both balls are identical in mass and the movie was filmed at 25 frames/sec. The text books are wrong again since the incident ball follows through after the collision. This time the COR is close to 1.0 but the incident ball is rolling forward before the collision, keeps spinning after the collision, so it continues to roll forward after the collision. The text books would be correct if the balls collided in outer space, or were suspended as pendulum bobs in a frame as in “Newton’s cradle”, but in the real world of billiards there is an additional force on each ball due to friction with the table. The effect of friction can be seen by observing the ball that is initially at rest (by advancing the film one frame at a time). After the collision it starts sliding along the table without rotating but it starts to roll after it slides a few inches, due to friction at the bottom of the ball.

MovieB is more like the textbook model where the incident ball comes to a complete stop. To achieve this result, it is necessary to hit the incident ball towards the bottom of the ball so it is incident with backspin. Alternatively, you can play either film backwards and it will appear to obey the laws of physics. It doesn’t quite obey the laws of physics when played backwards since friction acts to decelerate rather than accelerate objects.

A very interesting and comprehensive web site devoted to the physics of billiard ball collisions has been set up by David Alciatore at http://www.engr.colostate.edu/pool

2. Squirt in billiards (August 2007)

Figure 1 shows a common situation in billiards where a moving ball strikes a stationary ball in such a way that one ball moves to the left and the other moves to the right. The angle between the two paths, after the collision, is always close to 90 degrees. The path taken by the ball that was initially at rest is along the line joining the ball centres when they first touch. The latter result arises because the friction force between two billiard balls is very small. The only significant force on the two balls is the one perpendicular to the two contacting surfaces, known as the normal reaction force. The stationary ball therefore accelerates in the direction of the normal reaction force and continues in that direction after the two balls lose contact.

Before the balls collide, there is no momentum in a direction perpendicular to the path of the incident ball. Momentum is conserved in that direction, so the total momentum in that direction, after the collision, is also zero. By assuming that the loss in energy during the collision is very small, it is not hard to show that the two balls must head off at right angles after the collision.

When a cue stick strikes a stationary ball, the result is quite different. Fig. 2a shows a typical situation where the ball is struck off-centre in order to impart sidespin. The ball heads off in a direction that is nearly but not exactly parallel to the initial direction of the cue. The deflection angle, known as the squirt angle, is typically only a few degrees. By contrast, when another billiard ball strikes a stationary ball, the stationary ball can "squirt" off at almost any angle up to 90 degrees, depending on the line of the incident ball. The difference is due to the friction force that acts on the ball in a direction parallel to the surface at the contact point. The coefficient of sliding friction (COF) between one ball and another is typically only about 0.06. The COF between a cue tip and the ball can be as high as 0.7, depending on the amount of chalk on the tip and other factors.

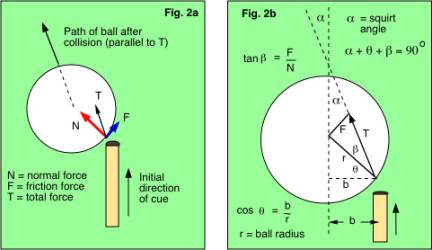
The force acting on the ball has two components. One is the normal reaction force, N, acting in a direction perpendicular the surface. The other is the friction force, F, acting parallel to the surface. The two forces together have a resultant or total value T which acts in the squirt direction - or vice versa. That is, the ball squirts in the direction of T. When the cue first strikes the ball, the tip will start sliding along the surface and then F = COF x N. The value of F could be as large as 0.7N, in which case the ball could potentially squirt off to the right rather than to left in Fig. 2a. However, the friction force does not remain this large for the whole collision time. The friction force on the ball causes the ball to start rotating, while the friction force on the tip (equal and opposite to that on the ball) causes the tip to slow down. When the ball rotates as fast as the sliding tip, sliding motion ceases and the tip grips the ball. The rotating ball then exerts a static friction force on the tip to the right and the tip exerts an equal and opposite force on the ball to the left. The friction force on the ball therefore reverses direction during the grip phase.

The average friction force on the ball, averaged over the whole collision time, will therefore be less than 0.7N, and may be as low as 0.3N or 0.4N. In fact, the squirt angle provides a direct measure of the average friction force. For example, suppose that in Fig. 2b the cue strikes the ball at b/r = 0.4 and that the average value of COF = F/N = 0.4. In that case, it is easy to show from the geometry that the squirt angle will be 1.8 degrees. At larger values of b/r, the cue tip will slide for a longer time before it grips the ball and then the average COF will be larger than 0.4. Conversely, at small values of b/r, the average value of the COF decreases, all the way to zero when b = 0. When b = 0, corresponding to the tip striking the centre of the ball, the squirt angle is zero since F = 0 and hence COF = F/N = 0.

A reversal in the direction of the friction force is a common effect that occurs whenever one object strikes another, but it is not well known and is rarely mentioned in text books. It occurs whenever a ball stikes a flat or a curved surface at an angle nearly perpendicular to the surface or at angles up to about 60 degrees away from the pendicular. In that case, the ball starts sliding along the surface but will then grip the surface when the relative speed of the two surfaces drops to zero as a result of rotation of the ball and/or the other surface. At glancing angles, the ball slides until it bounces, without gripping the surface.

If the ball is struck in the middle then there is no sidespin and the ball travels in the same direction as the cue. The cue itself continues to move along the same line as it was before it struck the ball. When the ball is struck slightly to the right of center, the ball is deflected slightly to the left and the cue tip is deflected to the right.

A more complete description is given in R. Cross, Cue and ball deflection (or “squirt”) in billiards, Am. J. Phys. 76, 205-212 (2008).

3. Gear Effect

A similar effect occurs in golf when a player mishits the ball by striking it off center. That is, the ball is struck not in the middle of the club face but toward one end of the club face. The result is that the club face rotates about an axis through the middle of the club face, causing the ball to squirt off to one side. The ball also develops sidespin. The two effects tend to cancel each other out. That is, the ball heads off to one side of the fairway but the spin of the ball causes it curve back toward the center of the fairway. In golf, this is described as the gear effect. The club face and the ball both rotate as if they were locked together as two gears. That is, they rotate in opposite directions. The two surfaces lock together or grip as a result of static friction. As the club head rotates, it exerts a friction force on the ball in a direction parallel to the face of the club. As a result, the ball is deflected in that direction (toward one side of the fairway) and it develops sidespin. In addition, there is a large force on the ball at right angles to the club face, which sends the ball on its way down the fairway.

The diagrams below shows how the gear effect operates when a golf ball strikes a block of wood off-centre and when a cue strikes a billiard ball off-centre. Further details of the gear effect are given in the Golf section. The bottom right diagram requires some explanation. The view of the ball and cue is from above the table, and the cue strikes the ball to the right of centre. The ball rotates in the direction shown (counter-clockwise viewed from above) since the cue tip starts sliding on the ball when it first contacts the ball, exerting a sideways friction force on the ball in the direction of the red arrow. When the surfaces of the ball and the cue tip are moving in that direction at the same speed, they lock together or grip. Since the heavy ball is now rotating, it drags the cue tip with it, and both move in the direction of the red arrow. The ball therefore exerts a force on the cue tip, in the direction of the red arrow, but the cue tip then exerts an equal and opposite force on the ball – in the OPPOSITE direction to that shown by the red arrow. The friction force therefore reverses direction on the ball when it changes from sliding to static friction. Sliding friction causes the ball to rotate counter-clockwise. The ball squirts in the direction shown as a result of the combined effects of the initial sliding friction force PLUS the subsequent static friction force PLUS the normal reaction force acting perpendicular to the surface of the ball PLUS the effect of friction of the table cloth on the spinning ball. The reversal in direction of the friction force was measured with an accelerometer for the case of the golf ball and wood block (middle diagram) and reported in Am. J. Phys 75, 658-664 (2007). It would be interesting to strike a billiard ball suspended as a pendulum bob in order to remove the effect of the table itself.

4. Squirt Movies

A Quicktime movie demonstrating squirt can be seen here. A cue was used to strike a 210 g block of wood inclined at 30 degrees to simulate the slope of a ball. The block squirts to the left and the cue deflected slightly to the right just before it was pulled back. The cue was withdrawn quickly to prevent the block hitting the cue as it spun around. An accelerometer on the end of the block showed that the impact lasted 2.8 ms.

When a billiard ball is used as a pendulum bob, it is easier to measure the ball spin since the ball doesn’t roll and spin at the same time. Results are shown here in the 10 deg squirt and 25 deg degree squirt movies.

The short movie shown here demonstrates a very interesting result. The movie was taken at 100 frames/sec, and is split into an upper part and a lower part taken 10 ms later. The ball is suspended as a pendulum bob above a ruler. Where the tip meets the ball at the contact point, several things happen in rapid succession, all within the 2 ms contact time. The tip first starts sliding on the ball. When the tip and the ball are moving at the same tangential speed, the tip grips the ball and both move at the same speed. Near the end of the contact period the contact force is no longer sufficient to maintain a firm grip, and the ball shoots out of the compressed tip. The tangential speed of the ball is then larger than the tangential speed of the tip so the tip slides backward relative to the ball at the end of the contact period. All that can’t really be seen on the film, but the film, plus other measurements of ball speed, spin and squirt angle, are all consistent with that interpretation.

Much higher speed squirt film can be seen on David Alciatore’s web site (also posted on YouTube).

5. Grip-Slip Movie

The bounce of a ball on a surface, or the impact of a bat or racquet or club with a ball, or the impact of a cue stick with a billiard ball, all involve initial slip, then grip, then backward slip. The result can be described in terms of a tangential coefficient of restitution, which is a number typically about 0.2 or 0.3. For a superball, it is more like 0.5 or 0.6. It is a number that represents how much of the stored elastic energy in the surface, due to stretching parallel to the surface, is recovered. If a lot of that energy is recovered, then the ball will spin rapidly when that energy is released. A simple example illustrating the process is shown in this Grip-slip Movie. The yellow bottle cap represents part of the surface of a ball. My hands represent say a cue stick. The metal rod represents the elastic part of the surface, which in this case would be the leather tip at the end of the cue. During the collision with a ball, the tip stretches in a direction parallel to the ball surface. Near the end of the collision, when the tip and the ball are separating, the elastic energy in the tip is suddenly released and the ball spins rapidly. Since the ball surface moves faster than the cue itself, (my hands) at this time, the cue appears to slide backwards relative to the ball.