PHYSICS OF GOLF

Rod Cross, Sydney University, July 2006

Most physics and biomechanics studies of a golf swing are concerned with the motion of a double pendulum. An experimental double pendulum is demonstrated here.

The most important shot in golf is the putt. If it takes 2 or 3 shots to get to the green and another 3 to sink the ball, then the average player will be disappointed with the putting effort. An interesting question is whether the chance of putting the ball is mostly in the hands of the player, or whether the result represents a certain amount of skill plus a certain amount of luck plus a certain amount of technology built into the putter. If the ball does not collide with the centre of mass of the putter (it rarely does) then the ball will tend to come off the putter at an unexpected angle, as shown in the movie of a superball colliding with a block of wood. See also the gear effect movies below for a golf ball impact on the same block of wood.

There are other factors that affect the trajectory of the ball on the way to the hole, such as the slope of the green, as described by Raymond Penner in the Canadian Journal of Physics, Vol 80, (2002), page 83-96. It is perhaps surprising that it is easier to sink a downhill putt than an uphill putt, but the reason is simple. The ball curves towards the hole when rolling downhill, but it curves away from the hole when rolling uphill. The consequences of missing a downhill putt are worse.

1. THE DIMPLED BALL PROBLEM

There is an even more obvious reason why golfers often have trouble sinking a putt. That is, golf balls are not perfectly spherical. They are covered in dimples, so the surface is quite uneven. As a result, the ball can bounce off a putter at yet another unexpected angle. To investigate this effect, I dropped a golf ball vertically onto a flat, horizontal slab of concrete to see if it always bounced vertically. Sometimes it did, but sometimes it didn’t. The top surface of the concrete was much smoother than the ball, so non-vertical bounces can be attributed to the uneven surface of the ball rather than any imperfections in the surface itself. A non-vertical bounce would be expected if the surface was not exactly horizontal, or if the ball was not dropped vertically, or if the incident ball was spinning, but (a) the surface was levelled with a spirit level, (b) the path of the ball was exactly parallel to a vertical plumbob line and (c) the incident ball had zero spin. Most of the time, the ball bounced within one degree of the vertical, but a one degree error is quite large in this context.

For example, consider a 10 ft putt. The hole has a radius of 5.4 cm and is 304.8 cm away. On a perfectly level surface, the ball has to be aimed within 1.0 degree of the line joining the centre of the ball and the centre of the hole. To sink a 20 foot putt, the required angle drops to 0.5 degrees.

QuickTime Movie A shows a ball bouncing about 1 degree to the left, and movie B shows a ball bouncing about 1 degree to the right. The ball was dropped from a height of about 80 cm. The ball is slightly fuzzy since the ball moved about 5 mm during the 2ms exposure time, but it is clear that the ball dropped vertically without spin. The vertical white line in the movie is a plumbob. The yellow spirit level and the concrete slab both appear slightly curved in the movie but that is an effect that occurs with most camera lenses and is known as barrel distortion. It is worst near the edges of the film.

After the bounce, the ball acquired a small amount of spin, consistent with the the fact that a horizontal force acted on the bottom of the ball pushing it sideways. Such a force can arise if there are more “hills” or protruberances on one side of the ball in contact with the surface than on the other side. Each hill can be envisaged as an object pointing out from the ball along a radius, and each hill will tend to push both downwards and sideways on the surface. Within the contact area there might be say 10 dimples on the left side and 10.5 dimples on the right side, depending on the exact alignment of the ball, but that could be enough to change the bounce angle by about 1 degree. The effect would be much more obvious and troublesome if there were say only 20 dimples on a golf ball and if each dimple were say 3 mm deep instead of a fraction of a mm.

There is another problem when putting. If the ball arrives at the hole too fast, it can bounce out of the hole when it strikes the opposite lip. This problem was analysed by Brian Holmes in the American Journal of Physics, Vol 59 (1991), page 129-136. Alternatively, the ball can run around the top of the hole and then jump out, as shown in the attached movie. Holmes analysed this situation too.

The end result is that professional golfers sink only about half of 6 ft putts, about 1/4 of 10 ft putts and only about 10% of 20 ft putts.

After I discovered in 2006 that golf balls don’t bounce like perfect spheres I found that another Aussie had already discovered this for himself a few years earlier. Slazenger markets his Bald Eagle golf ball which has some bald spots without any dimples. I have not seen or tested them but it sounds to me like a perfectly good solution.

The bad bounce problem is worst at low putting speeds and probably disappears when someone really whacks a ball since the dimples will then be squashed flat. At low putting speeds the sideways speed is then a bigger fraction of the desired speed so the ball will come off the putter with a bigger error in the launch angle.

Low speed tests are shown in Movie A, Movie B , Movie C and Movie D where I dropped a ball bearing (A) and a golf ball (B, C, D) onto a horizontal slab of polished granite. The camera was tilted slightly but the slab was accurately horizontal. The ball bearing bounced up and down on the same spot but the golf ball wandered across the slab after a few good bounces on the same spot. If I was a golfer (I’m not) it would probably give me the yips.

2. DOES A GOLF BALL ROLL IN A STRAIGHT LINE?

Given the dimple problem, it is not surprising that golf balls don’t roll along a straight line even on a perfectly flat, horizontal surface. Instead, the ball gets deflected slightly to the left or right on a random basis as it encounters each new dimple. The accumulation of random deflections can lead to a large deflection to the left or right, but it can also lead to a path that is essentially straight.

Several QuickTime, 1 Mb movies showing this effect are attached for balls rolling on a 13 mm thick, 66 cm diameter horizontal glass plate (with coloured paper underneath to indicate a straight line path).

Movie 1 : Pool ball rolls along a straight line. I was intruiged by the sound of the rolling ball. It generates a strong signal at 500 Hz (plus other frequencies) which is presumably one of the vibration modes of the glass plate. Car tyres and train wheels generate a similar sound when they roll.

Movie 2 : Ball bearing rolls along a straight line.

Movie 3 : Golf ball rolls to the left.

Movie 4 : Golf ball rolls to the right.

Movie 5 : Golf ball rolls along a straight line (on average).

The effect of many small sideways impulses is reduced when a golf ball rolls on surface with greater friction since the surface then reacts by pushing back on the ball. On glass there is very little surface friction to prevent the sideways motion. Another movie is attached showing a golf ball rolling on felt. The sideways deflection is much reduced but it is still evident to a small extent. The ball also slows down faster .

Movie 6 : Golf ball rolling on felt.

There is another potential problem in getting the ball to roll along a straight line. If one side of the ball is slightly heavier than the other side then the ball will curve towards the heavy side. You can prove this for yourself by adding a small weight (eg gum or blu-tack) to one side of the ball. The ball will then roll like a coin on its edge or like a ball used in lawn bowls.

An article (2Mb pdf) on the above tests was published in the Australian Golf Digest in Dec 2006.

3. PUTTING TESTS

The bounce angle off a putter is not the same as the bounce angle of a ball dropped onto a heavy surface since the putter tends to push the ball in the direction that the putter is moving (see Appendix below). To test this effect, I swung a mechanical putter at a ball suspended as a pendulum so that the rolling problem itself would be eliminated. The putter was made from a 66 cm long, 20 mm square aluminium bar suspended to swing freely as a pendulum. The ball was struck at low speed, as in a 2 or 3 ft putt, and swung horizontally by 58 cm to a scale where I could measure the sideways deflection. 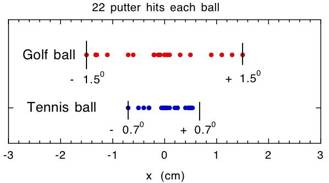A 1.5 cm deflection over a distance of 58 cm corresponds to a 1.5 degree error in the putting angle. That was the maximum error I observed in 22 separate putts.

The results are shown in a graph where I also compare results when putting a tennis ball 22 times with the same putter. For the tennis ball the worst error was 0.7 degrees. Film of the experiment is shown for GolfPutt1, GolfPutt2 and TennisPutt1. Each ball was suspended from the ceiling by a 1.6 m long cotton thread tied to a small eye hook screwed into the ball.

4. THE DIMPLED BALL SOLUTION

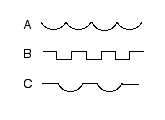
Given that dimples are good for aerodynamics and bad for putting, there is a need for a solution to this problem. One possibility would be to make golf balls more spherical, by changing the dimple pattern. For example, consider the following dimple patterns. A is the conventional pattern, while B and C are alternative patterns that leave a greater fraction of the spherical surface untouched by dimples. It should be possible to produce a ball like this with good lift and drag properties and with improved putting properties, by fiddling with the depth and spacing of the dimples.

A much simpler and much more logical solution would be to allow players to use different balls in the same way as they are allowed to use different clubs for each different shot. Given that players are allowed to pick up the ball when it gets to the green, it would be a simple matter when they change their club to a putter to change the ball to a smooth sphere. The point of changing the club is to make it easier for the player to hit the ball into the hole. In that case, why not change the ball as well? It makes no sense at all to use a dimpled ball for putting, unless the purpose of the rules of the game is to make it as difficult as possible for players to sink a put. In that case, it would make more sense to make the hole smaller.

5. THE GEAR EFFECT

The gear effect is important in golf since it allows golfers to spin the ball in a direction that one would not normally expect. It allows players to putt the ball with early topspin (or with less backspin) and it is the basis of the curved face of a driver. The point of the curved face, as opposed to a flat face, is that it provides an automatic side spin correction when a player strikes the ball off-centre. Side spin acts to curve the ball back towards the centre of the fairway during flight even if the ball is headed away from the centre when it is struck.

The gear effect describes what happens when one gear turns another. If one gear wheel turns clockwise then the other turns counter-clockwise. A similar thing can happen if the face of a golf club moves across the face of a golf ball. That is, if the head rotates clockwise then it can “engage” the ball to spin it counter-clockwise. If the club head strikes the ball at a point that is not in the centre of the club head then the force of the ball pushing against the face can cause the head (and the shaft) to rotate about the centre of mass of the head. As a result, the face can move across the ball while it simultaneously moves forward towards the target.

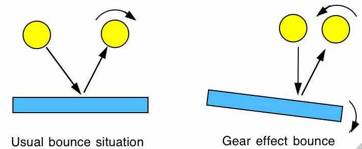
The diagram below shows two bounce situations. The diagram on the left shows the usual situation where a ball is thrown obliquely to the ground without spin. The ball then bounces spinning clockwise as a result of the friction force acting to the left, parallel to the ground. If the ball is incident at right angles to the ground, then the ball bounces without spin. We can describe a bounce off the ground as the “usual” bounce situation where the outgoing spin of the ball depends on the angle of incidence and where the bounce surface itself does not move.

If the bounce surface itself rotates, the ball can bounce in the expected direction but spin in the opposite direction. This is the situation shown on the right, where the ball impacts off-centre on a surface and causes the surface itself to rotate. The surface here could be the face of a club or the strings of a tennis racquet. If we imagine that the ball and the surface engage as gears, then the ball will rotate in the opposite direction to the surface. Penner analysed the situation for a golf club in Am J Phys 69, 1073-1081 (2001). Alan Nathan and I analysed the gear effect on a block of wood in Am. J. Phys. 75, 658-664 (2007). See also the discussion on squirt in billiards (Billiards page) which is also an example of the gear effect.

Golf balls and clubs don’t actually have gear teeth that mesh together in the conventional way, but the result is the same since the surfaces of balls and clubs are rough at a microscopic level. Two surfaces in firm contact with each other can therefore lock together or grip as a result of static friction, which is exactly what happens to the bottom of your shoe when you walk on a non-slippery surface. Walking on ice is more difficult because there is very little grip or friction on ice.

To examine the gear effect, I filmed a golf ball swinging as a pendulum bob towards a block of wood which was allowed to slide on a sheet of black cardboard on a table. The bottom of the ball was about 1 mm above the cardboard at its lowest point so it could swing freely. In the real world the club approaches the ball but the physics is exactly the same if the ball approaches the club. It is the same collision, viewed in a different reference frame (see Appendix). In my case it was simpler to swing the ball rather than the block of wood.

Six different results are shown, as follows:

Movie 1. Ball impacts near centre of block and bounces without spinning.

Movie 2. Ball impacts near centre of block when block is inclined. The ball bounces off spinning in the “usual” direction, but the gear effect adds to the spin since the block rotated slightly.

Movie 3. Ball impacts near centre of block inclined the other way. The ball spins in the “usual” way. There is no gear effect here since the block did not rotate.

Movie 4. Ball impacts at right angles towards edge of block. Ball spin is due entirely to the gear effect.

Movie 5. Ball impacts towards edge with block inclined. Gear effect adds to the “usual” spin.

Movie 6. Ball impacts towards edge of block when block is inclined the other way. In this case the gear effect reduces the “usual” amount of spin. If the block was clamped so it could not rotate then the ball would spin clockwise when it bounced. Since the block does rotate, it exerts a counter-clockwise torque on the ball, thereby reducing the outgoing spin.

A much simpler example of the gear effect is shown in the attached movie where a tennis ball is resting on surface at rest. The surface is then accelerated to the left (by a mass and pulley system) resulting in clockwise (gear effect) rotation of the ball. After the surface comes to a stop the ball rolls back to where it was. The interesting physics question here is whether the ball rolls or slides on the surface or whether it does a bit of both. At low surface speeds the surfaces lock together like gears as a result of static friction. The ball then rolls on the surface. At sufficiently high values of surface acceleration, static friction will no longer be enough to lock the surfaces together and the surfaces will slide past each other. The ball will still rotate, but the mechanism will be due to sliding friction rather than the interlocking gears effect.

6. GEAR EFFECT OFF A MOVING PLATFORM

A simple way to understand the gear effect is to consider the bounce of a ball off a moving platform. This is a case of practical importance in tennis or baseball where a ball bounces off a moving racquet or bat. Three movies are shown where:

1. Platform is at rest and ball bounces with topspin.

2. Platform is moving at same speed as ball and ball bounces with zero spin.

3. Platform is moving faster than the ball. The ball bounces with backspin, which is what one would expect if the ball and the platform engaged as gears.

The gear effect occurs here because I am moving the platform. In golf, it is the ball itself that causes the platform (ie the club head) to move in a direction parallel to the surface of the club.

To a physicist, all three movies here are essentially the same movie but viewed in different reference frames. I could have moved the camera instead of the platform and produced the three movies that way. For example, the second movie shows the platform moving at the same speed as the ball. If I had also moved the camera at that speed then I would see the ball falling vertically onto a stationary platform in which case the ball would bounce vertically without spin.

6A. APPENDIX: ANGLE OFF PUTTER

Suppose that a golf ball approaches a putter at 5 m/s when the putter is initially at rest. Suppose also that the ball bounces off the putter at 2.2 m/s at an angle of 26 degrees to the perpendicular. In that case, the bounce speed perpendicular to the putter face is 2 m/s and the bounce speed parallel to the putter face is 1 m/s. No golf ball would bounce at such a large angle off the putter but the point of this exercise is to show that the angle reduces when the putter strikes the ball. If the ball is initially at rest and the putter approaches the ball at 5 m/s, then the ball will be launched at 7.1 m/s at an angle of 8 degrees to the perpendicular.

Both situations are shown in the diagram below. Diagram (1) shows the ball approaching the putter at 5 m/s and diagram (2) shows the ball bouncing off the putter at 2.2 m/s. A bug is flying beside the ball at 5 m/s to keep an eye on things. As far as the bug is concerned, the ball is not moving at all and the putter is approaching the ball at 5 m/s, as shown in diagram (3). After the collision, the bug sees the result shown in diagram (4).

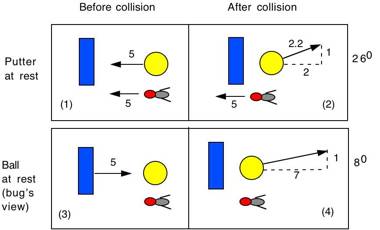
In diagram (2), the ball travels east at 2 m/s and north at 1 m/s. The bug is travelling west at 5 m/s so it sees the ball travelling east at 5 + 2 = 7 m/s with respect to the bug. It sees the ball headed north at 1 m/s. That is the situation shown in diagram (4). As far as the bug is concerned, the ball comes off the putter at an angle of 8 degrees, while a person standing beside the stationary putter in diagram (1) would see the ball bounce off at 26 degrees. It is exactly the same collision. The ball speed and bounce angle depend on the frame of reference. The bounce angle off a moving putter is therefore smaller than the bounce angle off a putter at rest, by a factor of about 3.

7. SWEET SPOT OF A GOLF CLUB

The sweet spot of a golf club is right in the middle of the front face. A ball struck with the heel or toe of the club feels bad, and the result is that ball heads off at an angle to the intended angle. If the club head swings along a certain path and contacts the ball in line with its centre of mass, then the club head will continue along that path without being deflected. There is then no wobble of the head and the shot feels nice.

A simple demonstration of this effect is to throw a ball at a putter that is held by one hand. Throw the ball with the other hand to impact at the toe, heel or middle of the club face. The results can be seen in the TOE Movie and the HEEL Movie. The amount of wobble depends on how firmly you grip the handle. The wobble period is about 50 ms, and it can be seen clearly in the Toe and Heel Movies. There is no wobble in the Sweet Spot movie. The same effect would arise if the club handle was supported by a spring. In this case, the spring was the muscles and tendons in my arm. My muscles told me when I struck the sweet spot, and so did a small accelerometer mounted on the club head. In fact, it is really neat to locate the sweet spot this way. Of all the various signals picked up by the accelerometer, the one that most obviously correlates with the feel of the club is the 20 Hz wobble. It is the smallest of all the various components of the acceleration since the frequency is so low. The acceleration is quite small (after the 1ms impact is over) but the movement of the head (in mm) is large. High frequency vibrations are much larger in terms of the acceleration of the club but they have a much smaller effect on the muscles in the arm.