“Simple”
Collisions
Rod Cross, Sydney University
Collisions in physics are never as simple
as they seem, even the simplest ones. That’s why they are so interesting.
1. Head-on Collisions
Suppose that ball A collides head on with ball B. Ball A has mass Ma and ball B has mass Mb.
Ball A has speed Vo before the collision and ball B is at rest.
After the collision, ball A has speed Va and ball B has speed Vb.

It is shown in elementary physics text books that:
(1) If A is heavier than B then A will slow down
during the collision but it will keep moving forward at reduced speed after the
collision, with Va < Vo. This happens when A is a bat
and B is a ball.
(2) If A
and B have the same mass then A will come to a complete stop and B will acquire
speed Vo (as often observed with colliding billiard balls).
(3) If A is lighter than B then A will bounce backward
off A so Va < 0. This happens when A is a ball and B is a bat.
We can use this result to see if a baseball is heavier
or lighter than a cricket ball.
Of course we could just weigh them to find out, but it is much more
interesting to collide them together. This type of experiment was
popular in the 17th Century, when physicists like Newton, Descartes,
Huygens, Leibniz and Wren were
trying to figure out whether momentum (mv) was conserved, whether the vis viva
(mv2) was conserved, whether mv was more important than mv2 and
how they were related to force. They argued with each other for 50 years,
without fully understanding the modern concept of energy. Given the historical
importance of these arguments, it is worth while spending a short time with a
video camera to get a better feel for the problems they faced. To do so, we can
pit the national pastimes of the USA (baseball and basketball) against the
national obsessions of the British (cricket and soccer) to see who uses the
heaviest balls.
The first movie shows a
cricket ball hitting a stationary baseball, each mounted as a pendulum. The
cricket ball continues in the same direction after the collision (it follows
through), indicating that the cricket ball is heavier than the baseball.
The second movie shows
the same baseball hitting the same cricket ball when the cricket ball is at
rest. This time the baseball continues in the same direction, indicating that
the baseball is heavier than the cricket ball.
Obviously, something is wrong with the textbook model
of the collision. Newton figured out that the relative speed after the
collision is a fixed fraction of the relative speed before the collision,
regardless of which ball is at rest before the collision (and even if both
balls are headed toward each other). He called that fraction the coefficient of
restitution (COR). That is,
COR
= (Vb – Va)/Vo
You can use the film to see if he was right and to
determine which ball is the heavier. The text book calculation is correct only
if COR = 1, meaning that there is no loss of energy during the collision.
Visual inspection of the film suggests that they each have about the same mass.
Newton didn’t have a video camera or a baseball. He measured ball speed in
terms of the amplitude of the pendulum swing, using balls made from compressed
wool, steel, cork and glass. The relevant formula, if you need it, is
here: Formula
2. Billiard Ball Collisions
MovieA shows a typical
head-on collision between two billiard balls when one is initially at rest.
Both balls are identical in mass and the movie was filmed at 25 frames/sec. The
text books are wrong again since the incident ball follows through after the
collision. This time the COR is close to 1.0 but the incident ball is rolling forward
before the collision, keeps spinning after the collision, so it continues to
roll forward after the collision. The text books would be correct if the balls
collided in outer space, or were suspended as pendulum bobs in a frame as in “Newton’s cradle”, but in the real
world of billiards there is an additional force on each ball due to friction
with the table. The effect of friction can be seen by observing the ball that
is initially at rest (by advancing the film one frame at a time). After the collision
it starts sliding along the table without rotating but it starts to roll after
it slides a few inches, due to friction at the bottom of the ball.
MovieB is more like the
textbook model where the incident ball comes to a complete stop. To achieve
this result, it is necessary to hit the incident ball towards the bottom of the
ball so it is incident with backspin. Alternatively, you can play either film
backwards and it will appear to obey the laws of physics. It doesn’t quite obey
the laws of physics when played backwards since friction acts to decelerate
rather than accelerate objects.
A very interesting and comprehensive web site devoted
to the physics of billiard ball collisions has been set up by David Alciatore
at http://www.engr.colostate.edu/pool
and at http://www.dr-dave-billiards.com
Here are two more collisions between balls of equal
mass, where I hold one ball to increase its mass. The first is with two pool
balls. The second is with two tennis balls. See if you can predict the result
in each case. In theory, a light
ball should bounce off a heavy ball when the heavy ball is at rest.
Then click on the photos to see the results. In the
first case there are two collisions, first between the two pool balls and then
between the struck ball and my soft hand. In the second case there is only one
collision since a tennis ball is about as soft as my hand.
3. Oblique Collisions (Sept 2007)
Most collisions in sport are not head-on. Rather, objects usually collide at an angle.
Examples are a bat and a ball or a tennis ball bouncing off the court.
Furthermore, the ball is usually spinning before it bounces, and then changes
its spin after the bounce. Suppose
a tennis ball collides with the court at a certain speed, spin and angle. If we
know how well the ball bounces (as measured by its coefficient of restitution)
and if we know the friction force on the ball (as measured by the coefficient
of friction) then we can calculate the rebound speed, spin and angle of the
ball. The tricky part is to
determine the friction force. The problem is, the ball can slide on the court
or it can grip the court or it can start to slide then grip then slide again
before it bounces. Not much is known about these effects. A simple way of
measuring the friction force is described below. Sufficient details are given
so you can measure the friction force yourself if you are so inclined and have suitable
equipment. I find it surprising that we know so much about the behaviour of the
stars and planets and atoms and molecules, and still know so little about the
behaviour of a bouncing ball.
When a tennis ball bounces on the court, the force acting
on the ball at right angles to the court is called the normal reaction force N.
The force acting on the bottom of the ball, parallel to the court surface, is
the friction force F. Friction acts to slow down the ball and to change its
spin (due to the torque on the ball). If the ball slides along the court during
the bounce, then F is typically about 0.7N where the 0.7 factor is the
coefficient of sliding friction (COF). But if the ball is incident nearly at
right angles to the court, or to the strings of the racquet, then the ball will
grip the court or the strings at some stage during the bounce, perhaps right from the start. If the
ball is incident at a small enough angle, with tan(Angle) < COF, then the ball grips from the start
without an initial period of sliding. There must be a small sliding period
where the bottom one gram of ball slides to a stop, but the rest of the ball
can keep moving forward since the ball is elastic and will stretch during the
bounce. Measured values of F and N
are shown in the graphs below.
The following two movies show a hollow yellow rubber
tennis ball, without its cloth cover,
bouncing off a 450 gram solid block of glass. The front edge of the
glass block is hard to see but is level with the vertical black line on the
scale. Taped to the rear side of the glass is a thin piezo disk used to measure
the acceleration of the block at right angles to the surface. It therefore
measures the normal force, N. Taped to the end of the block is an identical
accelerometer that measures the acceleration at right angles to N. It therefore
measures the friction force F. The block of glass is on a sheet of slippery
teflon but it still slides to a stop fairly quickly after the collision. The
piezo disks are too thin (only 0.3 mm) to see in the movies, but the thin wire
leads to each disk can be seen as well as the voltage probes. Each disk outputs
a voltage when it accelerates or when a force is applied at right angles to the
disk. They are the same piezo disks as those used in musical greeting cards,
only 15 mm in diameter instead of 19 mm.
Two collisions were filmed, both with the rubber ball
mounted on the end of a length of cotton thread as a pendulum. In both cases,
the ball was incident at about 20 degrees to the normal. In one case the ball
was incident without spin. In the other case, the ball was incident with
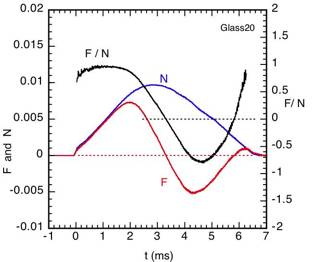
backspin (spinning clockwise). The ball incident without spin gripped the glass
right at the start, with the result that F/N was only about 0.4 at the start of
the collision. A similar situation
arises if a pencil eraser is pushed obliquely onto the top of a table. It tends
to grip the table without sliding, and distorts elastically as it does so. Grip
arises as a result of static friction. It allows you to walk on the ground
without slipping, and it allows the leather tip of a billiards cue to grip a
billiard ball without sliding across the ball.
The ball incident with backspin started sliding across
the glass, with F/N about 1.0, but it then gripped the glass. During the collision, the friction
force reversed direction a few times because the rubber ball vibrated back and
forth a few times in a direction parallel to the surface of the glass, while
the contact region remained stuck to the glass. The whole ball may not have
vibrated this way, but at least part of the ball near the contact region
vibrated. As it did so, the whole ball compressed for the first 3 ms and then
expanded back to its normal shape during the next 3 ms. The ball remained in
contact with the glass for 6 ms. The results of the F and N measurements, and
the calculated F/N ratios are shown below.
A solid ball (eg baseball, golf ball, superball etc)
typically has only one reversal in the direction of F if it grips a surface
when it bounces. A hollow ball (such as a football or basketball or tennis
ball) can have several reversals in F while it bounces, because such a ball is
relatively soft and has a relatively long contact period with the ground.
(A) Ball incident without spin (see Movie here)
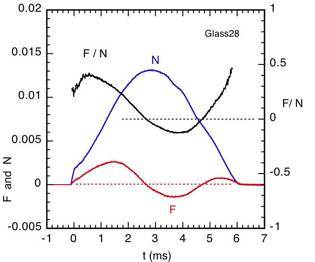
(B) Ball incident with backspin (see Movie here).
The ball incident with backspin slides at the start
because the surface of the ball is moving too fast to grip the glass. As the
ball slides, the contact point slows down due to sliding friction, and then
grips when the contact point comes to rest on the surface. Essentially the same
effect arises if the ball is incident without spin but at a larger angle to the
normal. That is, the ball slides for a short period (with F/N = coeff of
sliding friction) and then grips the surface. At glancing angles, the ball
slides for the whole contact period without gripping the surface.
4. Collision of a ball with a bat, racquet or club
A collision between a ball and a bat or racquet or
club can be studied in a reference frame where the bat, racquet or club is
initially at rest. The physics of the collision is the same regardless of
whether the ball is initially at rest or the bat is initially at rest or
whether both are moving toward each other. Any one result leads directly to
another simply by changing the reference frame.
A brief description of the physics can be found here.
The essence of the problem can be studied by colliding
a ball with a block of wood. Two small movies are attached where a red
superball rolls along a horizontal surface and collides with a block of wood
that is heavier than the ball. Movie A shows what
happens when the ball collides in line with the centre of mass of the block. Movie B shows what happens when the ball collides
at a point that does not coincide with the CM, which is the usual situation in
baseball, tennis or golf. The block of wood comes to rest quickly after the
collision because of friction with the horizontal surface.
When the ball is incident at right angles and collides
with the middle of the block, the ball retraces its path at reduced speed. The block recoils along the same path as
the incident ball, without rotating. In movie B, the block recoils as before
but it also rotates, causing the ball to come off at an angle to the incident
path. Furthermore, the outgoing speed of the ball is reduced since it gives the
block some rotational energy as well as translational energy. A golfer trying
to hit a put or any other shot will therefore find that the ball comes off the
club at an unexpected angle if he or she does not take into account rotation of
the club in the hand. Similarly, a
tennis player can hit the ball too high over the net or into the bottom of the
net if the ball strikes the racquet off-axis.
The two movies are deceptively simple. They appear to
be almost trivial and not even worth thinking about. Nevertheless, it is quite
a challenging problem to work out say the rebound speed and angle of the ball,
even for something as simple as a rectangular block of wood. It gets even
harder if one takes into account the fact that the block vibrates when it is
struck, and that the energy loss due to vibrations depends on the impact point.
There are many questions that one can ask about this problem, none of which
have immediately obvious answers. For example, does the rebound angle for an
off-centre impact depend on the speed of the incoming ball (or the speed of the
bat or racquet or club as it approaches the ball)? If you have access to a
ball, a block of wood and a video camera, then you can repeat this experiment
and find out the answer to this and to many other questions. For example, what
happens when the incident ball is spinning or is incident at some angle other
than a right angle?
These are the sorts of questions that are asked by
bat, club and racquet manufacturers. They spend millions of dollars every year
searching for answers so that players can have access to the latest models to
help improve their game. In effect, the manufacturers work out the best shape
and weight of the wood block so that a player can swing it at the ball to
achieve the best result. In general, players like implements that are both
light and powerful, despite the fact that physics indicates that power is
proportional to the swing weight
(the moment of inertia) of the implement. In general, swing weight increases
with mass but it also depends on how the mass is distributed. If most of the
mass is at the far end (as it is in a golf club or a baseball bat) then the
swing weight will be a lot larger than if most of the mass was near the handle
end. If the swing weight is increased then the object will be harder to swing
but it will have more “built-in” power.
5. COLLIDING RODS
A head-on collision between two rods is another famous example where masses
don’t collide in the expected way.
If the mass and length of each rod is the same then the rods bounce as
expected, as shown in this Movie.
The incident rod comes to a stop if the second rod is intially at rest, just
like in the text books. But if the stationary rod is longer and heavier than
the incident rod, then the incident rod STILL comes to a stop! Not only that,
the long rod rings like a chime. The sound of the impact is completely
different. See the second Movie.
What happens if the heavier rod hits the light rod when the light rod is at
rest? Give up already? Then you can see what happens here.
David Auerbach’s article in Am J Phys, 62, 522-525 (1994) provides the
explanations. A collision with a long rod is less efficient since vibration
energy is retained in the long rod after the two rods separate. A similar
effect occurs when two springs collide. If you think of a rod as a series of
masses connected by springs, then it is easy to see how a vibration wave can
propagate along the rod and how that vibration can persist even after the rods
separate. In that case, the collision is one where momentum is conserved but
the kinetic energy after the collision is less than the kinetic energy before
the collision, unless the rods are equal in length.

