Ball spin off tennis strings

Updated September 2015

A major question in tennis is how the strings manage to reverse the direction of spin of the incoming ball, and how the process can be improved. The ball bounces off the court with topspin, but the player needs to reverse the spin direction in order to return the ball with topspin. The behaviour of a spinning ball is shown in the following four movies, each filmed at 600 frames/sec.

The first movie shows a spinning tennis ball dropped vertically onto a smooth table. The friction force at the bottom of the ball pushes the ball sideways and it reduces the spin. The friction force is not large enough to reverse the spin. The second movie shows a spinning superball dropped vertically onto the table. The friction force pushes the ball sideways and it also reverses the spin direction.

A superball is more elastic than a tennis ball, in both the vertical and horizontal directions. Tennis strings are also highly elastic in both the perpendicular and tangential directions. The following two movies show a spinning tennis ball incident on four parallel tennis strings. In the first movie, the ball is incident at right angles to the strings. In the second movie it is incident at 30 degrees to the perpendicular. In the latter case, the strings behave like a superball in reversing the spin direction. If you examine the behaviour of each string (advancing one frame at a time) you can see what each string is doing and how the strings manage to reverse the spin direction. The strings are not pushing in a direction through the middle of the ball, so they exert a torque that causes the ball to reverse its spin direction.

Generation of ball spin

Rod Cross, Physics Dept, Sydney University. January 2011

Ball spin can be generated by hand or by striking the ball with an implement such as a billiard cue, or a bat or a racquet. The essence of the latter problem can be studied by bouncing a ball off a rigid surface. The graphs below show experimental data for a tennis ball incident without spin on a heavy slab of granite. The ball was incident at relatively low speed, about 6 m/s, but the ball was thrown by hand and the speed varied from about 5 m/s to about 7 m/s. The measured ball spin was divided by the actual incident speed then multipled by 6 to quote the spin value for a ball incident at 6 m/s. The slab was polished and relatively slippery, so the experiment was repeated by taping a sheet of P800 emery paper to the slab in order to compare rough and smooth surfaces. P800 is not very rough, and is a fine grained emery paper for polishing timber or metal. It also polished the ball each bounce, the ball leaving behind a yellow patch on the black paper (as can be seen in the following P800 video clip).

A few typical bounces can be seen here (Granite) , here (Granite) and here (P800), all filmed at 300 frames/s. It is not easy to throw a ball without spinning it. The ball will spin if the fingers drag up, down or across the back of the ball as it comes out of the hand, due to the tangential friction force between the ball and the fingers.

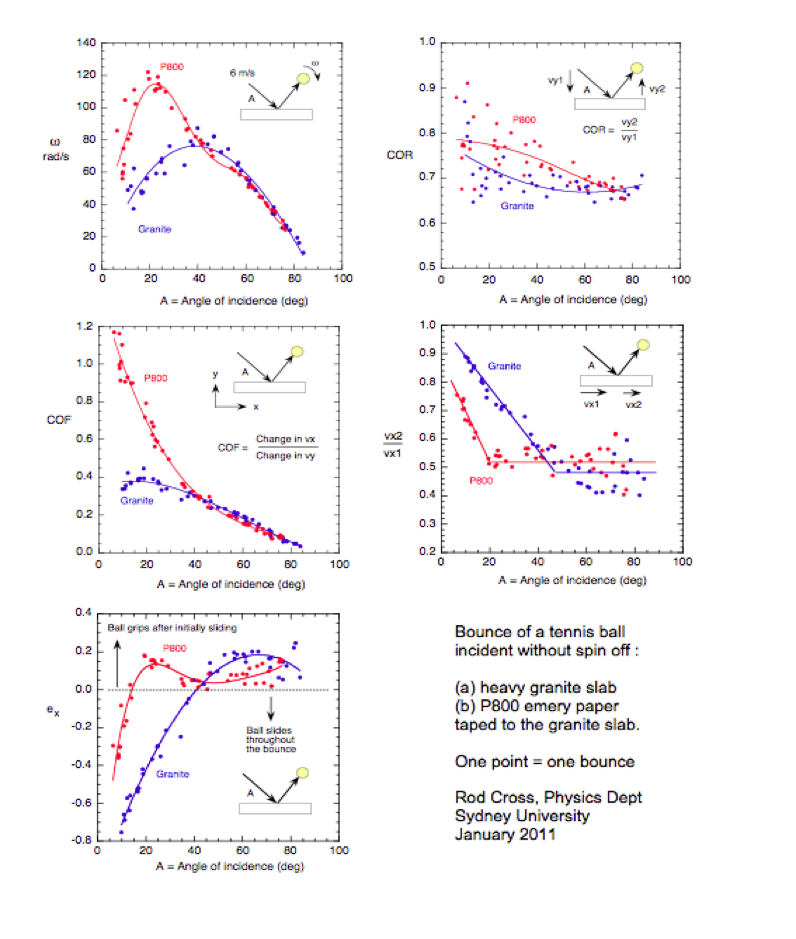
The quantities plotted in the various graphs were taken from measurements of

w = ball spin (in radians/sec) after the bounce

Vx1 = horizontal ball speed before the bounce

Vx2 = horizontal ball speed after the bounce

Vy1 = vertical ball speed before the bounce

Vy2 = vertical ball speed after the bounce

COR = coefficient of restitution = Vy2/Vy1

COF = coefficient of friction = (Vx1 – Vx2) / (Vy1 + Vy2) (both Vy’s taken as positive)

Ex = tangential coefficient of restitution = - (Vx2 – Rw) / Vx1 where R = ball radius = 0.033 m

Ex is similar to COR but it measures the ratio of the horizontal or peripheral speed of the ball at the contact point rather than the vertical speed ratio. For a superball, Ex is about 0.6. For most other balls Ex is about 0.1 or 0.2, with the result that other balls don’t spin as fast. However, Ex can be enhanced if the ball bounces off an elastic rather than a rigid surface, in which case the ball will spin faster. Explanations can be found in the book Technical Tennis and in some of the relevant ball bounce papers listed under Publications. The main points concerning ball spin are that it depends STRONGLY on (a) incident ball speed (b) incident angle and (c) incident ball spin, and it depends less strongly or only weakly on (d) coefficient of friction between the ball and the surface (e) elasticity of the ball (measured here by Ex) and (f) elasticity of the surface.

When a ball bounces off a surface, it starts by sliding. Friction slows it down, so Vx decreases. The torque due to friction acts to generate spin, so w increases as Vx decreases. At low values of A the ball slides the whole time so COF = coefficient of sliding friction and Ex is negative. At high values of A, Vx = Rw at some point during the bounce and then the ball grips the surface since the contact point comes to rest on the surface (as it does when a ball rolls on a surface). In that case, Ex becomes positive and the spin off a smooth surface is the same as the spin off a rough surface.