BALL TRAJECTORIES
Rod Cross, Updated June
2011
A pdf version of this file (but without
the movies) can be downloaded here.
The relevant aerodynamics, including a
tutorial on boundary layer separation and how it affects lift and drag on
sports balls, is described in this pdf file on sports
balls.
Wind tunnel photos of boundary layer
separation around various balls are included in this
pdf file. The pictures are worth thousands of words and show how the Magnus
force can sometimes be negative.
1. PROJECTING FOR
MAXIMUM DISTANCE
In some ball sports, a player will want to project
the ball as far as possible. The ball must then be launched as fast as
possible, but the interesting physics question concerns the best angle at which
to project the ball. For example, should a golfer hit the ball upwards at say
45 degrees to the horizontal or will the ball travel further if it is projected
at a lower angle? The same question arises in baseball if a player is trying to
hit a home run, or in cricket if a player is trying to hit a six over the
fence, or in a soccer throw or in football or when throwing a javelin or shot
put. Similarly, an athlete competing in the long jump needs to jump both
upwards and forwards, but what is the best launch angle above the horizontal?
There is no single answer here that covers all cases
but the problem can be viewed in the following way. When a ball is hit or
thrown for maximum distance then it travels in the horizontal direction at
speed V and it remains in the air for time T. The horizontal distance (D)
travelled before it lands is given by D = VT. For D to be as large as possible,
V and T both need to be as large as possible. V is a maximum when the ball is
projected as fast as possible in the horizontal direction. But then the ball
will fall to the ground quickly and T will be quite small. T is a maximum when
the ball is projected straight up in the air so it travels as high as possible,
but then the horizontal speed V is zero. The ball will spend a long time in the
air but it will travel up and down along the same vertical path and travel zero
distance horizontally.
If the only force acting on the ball is the force of
gravity and if the ball is projected from ground level and lands at ground
level then the ball will travel the greatest horizontal distance when it
projected at 45 degrees to the horizontal. That way, the vertical launch speed
is the same as the horizontal launch speed and it represents the best
compromise between maximising V and maximising T.
There are several reasons why 45 degrees is NOT the
best angle in practice. One is that the ball will also be be subject to a drag
force acting backwards on the ball due to air resistance. The drag force can be
bigger than the gravitational force if the ball is travelling fast enough,
although this situation would never arise when projecting a very heavy ball
such as the shot put. When the drag force is taken into account, maximum
distance requires that the launch angle is less than 45 degrees. As ball speed
increases, so does the drag force and the lower is the required launch angle. A
launch at 45 degrees would allow the ball to remain in the air for a longer
time, but it would then be launched at a lower horizontal speed at the start
and it would slow down more because of the longer flight time.
An additional aerodynamic force arises if the ball is
spinning. This force is called the Magnus force, it increases as the ball spin
is increased, and it acts at right angles to both the path of the ball and to
the rotation axis. For example,
when a golf ball is projected with backspin then the Magnus force acts upwards
on the ball as a lift force and holds the ball in the air for a longer time
than it otherwise would if it wasn't spinning. In that case, the ball will travel
the maximum horizontal distance before landing if it is launched at an angle of
around 10 or 20 degrees to the horizontal. If the ball has enough backspin so
that the Magnus force is greater than the force of gravity then the ball will
rise up at an angle greater than 20 degrees after it is launched.
In cases such as the shot put where the ball is
launched from a certain height above ground level, the best launch angle is
also less than 45 degrees. One way to understand this is to imagine that the
ball actually started at ground level with a 45 degree launch but after it
rises to the actual launch height it will be travelling at a smaller angle to
the horizontal. Alternatively, one can consider this situation as one where a
ball is launched from ground level but where it lands below ground level.
Suppose that someone throws a ball off a cliff or a tall building and wants it
to land as far out as possible. The landing point is then well below ground
level and the time in the air depends mainly on the time it takes to fall to
the bottom. There is no need to throw the ball at 45 degrees to gain extra
height if the extra time in the air is only a small fraction of the time taken
to fall to the bottom of the cliff or building. In that case, maximum distance is
achieved by throwing almost horizontally to maximise the horizontal launch
speed. The same reasoning applies if a person wants to jump off a tall cliff or
building and land as far out as possible.
The long jump is a case where the best launch angle
is about 25 degrees. In this case the athlete takes many running steps to build
up horizontal speed. The very last step is used to increase the vertical speed.
It is not physically possible to jump vertically in one step at the same
horizontal speed as the runup. The athlete could jump at 45 degrees using a
much slower runup but the jump distance would then be much smaller. The time in
the air is determined by the vertical jump speed, which cannot be increased
since only one step is taken to achieve that vertical speed. The only way to
increase the jump distance D is to to increase the horizontal launch speed, V,
by taking a long runup. Then D = VT where T is the time in the air. Actually, D
is a bit larger than this because the feet land ahead of the centre of mass and
because the centre of mass starts from a point in front of the feet at the
start of the jump.
In athletic events, there is another consideration.
That is, the force that can be applied in the horizontal direction is not the
same as the force that can be applied in the vertical direction. A ball can be
thrown faster in the horizontal direction than in the vertical direction.
Consequently, the best launch angle for the shot put or the javelin throw is
even lower than one might expect just from the aerodynamics of the problem.
2. DRAG FORCE
If a ball or any other object is moving at speed V
through the air, then the air exerts a backwards force on the ball called the
drag force. If the ball is moving vertically up then the drag force acts
vertically down (and vice versa). If the ball is moving forward in a horizontal
direction then the drag force acts backward in a horizontal direction. The
formula for the drag force is
F
= CD d A V2 /2
where CD is called the drag coefficient, d
is the density of the air and A is the cross-sectional area of the ball. For a
ball of radius R, A = 3.14R2. The value of d at 20 degrees
Centigrade is 1.21 kg/m3.
Unlike the gravity force, the drag force does not depend on the mass of
the ball. It depends only on its radius and speed. CD depends to
some extent on the surface roughness of the ball and it also depends on ball
speed.
For a circular disk, CD = 1.0. For a streamlined object, CD can be less than
0.1.
The value of CD is constant and equal to
about 0.5 for a sphere at low ball speeds but it can drop dramatically to
around 0.2 at high ball speeds. The drag force itself may or may not drop when
CD drops, since F is
proportional to V squared. The drop in CD occurs as a result of a
change from smooth or laminar air flow around the ball to a more turbulent
flow. The drop in CD is especially large on very smooth balls, is
smaller on slightly rough balls and does not occur at all for a tennis ball
since the ball surface is too rough. For a tennis ball, CD is about
0.55 regardless of ball speed, but it depends slightly on the smoothness or
roughness of the cloth surface. A fluffy ball will slow down faster, partly
because the drag coefficient is larger and partly because the ball diameter is
then larger.
The speed at which CD drops depends on the diameter of the
ball. It occurs at low ball speeds on large balls (such as a soccer ball) and
at high ball speeds for small balls (such as a golf ball). Golf balls are
slightly dimpled so that CD drops at a lower ball speed than it
would for a perfectly smooth ball. For example, CD drops to about
0.25 at speeds above 8 m/s for a soccer ball. For a golf ball, CD
drops to about 0.25 at speeds above 15 m/s and remains at 0.25 even at speeds
up to 70 m/s. When a golf ball is
struck at speeds of around 60 m/s, and at low launch angles, it travels further
in air than it would in a vacuum since the lift force due to its backspin holds
it in the air for a longer time. However, if the ball is struck at 45 degrees
then it will travel further in a vacuum than in air.
3. DRAG FORCE ON A PARTY BALLOON
The effect of the drag force is very noticeable on
balls or other objects that are relatively light. It is the drag force on a
leaf or a piece of paper that causes it to take a longer time to fall to the
ground than a heavy object. A 57 gm tennis ball slows down by about 25% from
the moment it is struck to the time it lands on the other side of the court.
Most players would not even notice that the ball slows down as it travels
through the air, but it does. A
ping-pong ball would not even make it over the net. The drag force on a ping-pong
ball is less than that on a larger tennis ball travelling at the same speed,
but the mass of a ping-pong ball is many times smaller and the drag force
therefore has a much bigger effect in slowing it down.
The effect of the drag force on a 20 cm diameter
balloon dropped from the ceiling in my office is shown in Movie A. For comparison, Movie B shows the same situation for a baseball
dropped from the ceiling. It is obvious that the balloon falls much more slowly
than the baseball. The acceleration of the baseball is essentially equal to 9.8
m/s2 during the whole time the ball
falls since the drag force is much smaller than the gravitational force on the
ball, at least at the relatively low drop speed seen in the movie. After falling
through a height of 2.5 m, the ball accelerated to a speed v = 7.0 m/s.
It was relatively easy to calculate the drag
coefficient for the balloon by measuring its speed as it fell. I wanted to
check whether the drag coefficient was about 0.5, as it is for all other
spherical objects travelling through the air at low speed. I chose to measure
it for a balloon since the effect is much easier to see and much easier to
measure than for a heavy ball. I also learnt a few interesting things along the
way, such as the fact that the air inside the balloon was a lot heavier than
the balloon itself. I also found that adding 7 gm of air to the balloon
increased its measured weight by only 0.25 gm since the buoyant force of the
air outside the balloon exerted an upwards force on the balloon that almost
cancelled the weight of the extra 7 gm of air added inside the balloon.
Results of the balloon drop experiment are shown in
the graphs of vertical position, speed and acceleration below. The mass of the
rubber plus a 2.13 gm nut attached to the balloon was 3.43 gm.
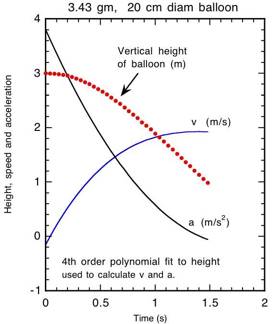
The balloon accelerated to 1.95 m/s after falling
through a height of 1.2 m and then the speed remained constant for the
remainder of its fall. It reached a constant speed called the terminal velocity
since at that point the total force on the ball dropped to zero. The force of
gravity acting down on the balloon was exactly balanced by the drag force
acting upwards and by the buoyant force of the air. In order to get a nice
vertical drop I needed to tie a 2.1 gm nut onto the bottom of the balloon using
a very light cotton thread.
Without the nut, the balloon tended to rotate and to veer off to one
side. The rubber balloon itself had a mass of only 1.3 gm but it was inflated
by adding 7.0 gm of air, so the total mass of the balloon plus the nut was 10.4
gm.
A tricky part of this experiment was working out how
much air I added. The mass of the inflated balloon was measured to be 1.55 gm
and its volume was approximately 0.00557 m3. The balloon was not exactly spherical
so I estimated its volume assuming that it was sphere of average radius 0.11 m.
The balloon was 20 cm in diameter across the long axis and 25 cm in diameter
along its long axis. The mass of
the displaced air was therefore 6.75 gm, which gives the buoyant force. In
other words, the mass of the inflated balloon was actually 1.55 + 6.75 = 8.3
gm. On the weighing scale it registered only 1.55 gm since the air exerted a
buoyant force lifting it up against the force of gravity.
Since the rubber itself had a mass of 1.3 gm, the air
inside the balloon had a mass of 7.0 gm. This is slightly larger than the mass
of the displaced air since the air inside the balloon was at a slightly higher
pressure.
The acceleration of the balloon as it was falling is
given by
F
= ma = mg - FB- FD
where FB is the buoyant force (mass of
displaced air times g) and FD is the drag force. At the start of the fall where V = 0,
the drag force is zero so a = g - FB /m. This works out to be 3.5
m/s2, which is close to the value 3.8 m/s2 that I
measured.
Terminal velocity is reached when a = 0 and then FD
= mg - FB. Using this formula I found that CD = 0.50,
which is the value expected for a slowly moving spherical ball. Part of the
reason that a balloon falls slowly is that the drag force slows it down, but
the buoyant force also plays a big role. Both of these forces are tiny compared
to the force of gravity on a baseball, although the drag force is important at
higher ball speeds than those shown in the baseball movie.
4. DRAG FORCE ON A BASEBALL
Consider a baseball of mass 145 gm and diameter 73
mm. If we take CD = 0.5
at low ball speeds then with A = 0.00418 m2 and d = 1.21 kg/m3, the drag force is
FD
= 0.00127 V2 (Newton)
while the gravitation force is mg = 0.145 x 9.8 =
1.42 Newton. At a ball speed V = 7 m/s, the drag force is only 0.062 Newton, 23
times smaller than the gravitational force. The two forces are equal at a speed
V = 33 m/s, which corresponds to the terminal velocity of a baseball dropped
from a great height.
5. MAGNUS FORCE ON A PARTY BALLOON
Most people who measure the Magnus force do so by
spinning a ball in a wind tunnel. The ball spins at a fixed location in the
wind tunnel while the air flows past it. An alternative way to measure the
Magnus force is to film the trajectory of a spinning ball using several
cameras, but a lot of cameras would be needed to view at right angles to a high
speed ball travelling over a distance of 50 m or more. At least one of the
cameras needs to film the ball at around 200 frames/sec or more to measure the
spin rate. Either way, measuring the Magnus force is usually a difficult and
expensive operation.
A conventional video camera can be used to film the
flight of a ball at low ball speeds and at low spin rates, but the Magnus force
is relatively small. To see any significant effect at low ball speeds one needs
a ball with a large surface area and a small mass. The obvious choice is a
balloon, although I have not seen any previous measurements for a balloon
myself. It turns out that a spinning balloon provides an excellent
demonstration of the Magnus effect since it is something that anyone can do
without needing expensive equipment and it is very easy to observe the effect.
The experiment is shown in Movie
A for a case where the balloon was spun clockwise, and in Movie B for a counter-clockwise spin. I removed the nut
at the bottom of the balloon for this experiment but I added a strip of white
adhesive tape around the circumference of the balloon to give it a bit more
rotational inertia and to help balance it. Without the tape, the balloon tended
to wobble and to twist around as it fell
The extra mass of the tape made it more stable and allowed it to spin
for a longer time without slowing down so rapidly. I ended up adding another
3.7 gm of string, wound three times around the circumference to reduce the
slowing down effect even further. In Movie A, the rotation rate dropped from
5.1 rev/sec to 3.3 rev/sec over 1.4 sec while the balloon fell to the floor.
Spinning a balloon by hand is not as easy as it
looks. I found that the best technique was to throw it upwards slightly as I
spun it. That way I was able to get the ball to drop vertically at the start so
I could more easily see the effect of the sideways Magnus force. The Magnus
force increases with both spin rate and with ball speed squared, so there is
essentially no sideways force at the start of the fall since the ball speed is
too low. As the ball fell towards the floor its spin rate decreased but its
speed increased, with the result that the ball deflected sideways in the
expected direction. The Magnus force acts on the whole ball in the same
direction as the direction of rotation of the leading (bottom) edge. If you are
very observant you will notice that the horizontal acceleration drops to zero
before the balloon hits the floor. The balloon coasts into the floor at
constant speed. The balloon is deflected a long way in the horizontal direction
over a relatively small drop distance. As a result, the drag force acting
backwards along the inclined path of the balloon has a horizontal component
that cancels the horizontal component of the Magnus force.
I was surprised that the spin rate decreased so
quickly. On heavier balls there is only a slight decrease in spin rate as the
ball travels through the air, although the effect has not been examined very
closely by anyone as far as I know. The effect is due to friction between the
air and the surface of the ball, and can be described in terms of the viscosity
of the air. If a ball starts spinning in a bucket of honey then it will stop
spinning very rapidly since honey is very viscous. Water has lower viscosity
(it pours more easily) and air has even lower viscosity. Neverthless, the
viscous force of the air acting on a ball as light as a balloon is enough to
stop it spinning after only a few seconds. The same viscous force would act on
any other ball of the same diameter and spin rate, but it would have a much
smaller effect on a heavy ball than on a light ball.
The Magnus force FM acting on a spinning
ball travelling at speed V is given by
FM
= CL d A V2 /2
where CL is called the lift coefficient, d
is the density of the air and A is the cross-sectional area of the ball. The
formula is essentially the same as that for the drag force but the lift
coefficient is generally smaller than the drag coefficient. The coefficient is
called a lift coefficient since the Magnus force is a vertical lift force on
say a golf ball moving horizontally with backspin. In fact, the Magnus force
acts horizontally on a ball moving vertically, and it acts vertically down on a
ball travelling horizontally with topspin. The Magnus force exists only if the
ball is spinning and it increases with the rate of spin. The formula here
doesn't show the spin effect, but CL depends on the rate of spin,
being roughly proportional to the rate of spin (and is zero when the spin is
zero). In the spinning balloon experiment, CL was about 0.1.
In the movie I am standing in front of all the issues
of The Physics Teacher and the American Journal of Physics since 1949. None of
those issues mention that the Magnus force is most easily observed with a
spinning balloon. It goes to show that there is still a lot of interesting
physics to be discovered in everyday objects.
The Magnus effect can even be seen with a rolled-up paper cylinder made from a single A4
sheet of paper. The one in the movie was 21 cm long, 9 cm in diameter and
joined with adhesive tape. I rolled it down an incline rather than spinning by
hand, otherwise I would have squashed the cylinder.
6. BASIC PHYSICS OF BALL TRAJECTORIES
When a ball or any other object is projected through
the air it will follow a curved trajectory until it hits the ground. The trajectory can be calculated easily
if we ignore air resistance and assume that the only force acting on the ball
is that due to gravity. The acceleration due to gravity is g = 9.8 m/s^2 and
the vertical force F acting on a ball of mass m is given by F = mg. In that
case, the horizontal speed of the ball through the air remains constant since
there is no horizontal force on the ball. Gravity acts only in the vertical
direction. The resulting ball path is then a parabola.
A ball projected vertically upwards at speed V will
rise to a height H where the potential energy mgH is equal to the intial
kinetic energy mV2 / 2.
Since mgH = m V2 / 2, we find that H = V2 / (2g) .
For example, if V = 1 m/s then H = 1/(2 x 9.8) = 0.051 m = 5.1 cm. If V = 10
m/s then H is 100 times larger, or 5.1 m.
If a ball is projected at speed V at an angle A to
the horizontal, then the horizontal launch speed is Vx = Vcos A and
the vertical launch speed is Vy = V sin A. At any time t after the
launch the horizontal (x) and vertical (y) positions of the ball will be given by the formula s = ut +
at2/2 where s = distance travelled, u = initial velocity and a =
acceleration. In this case,
x
= ( Vcos A) t
(a = 0 in the horizontal direction)
and
y
= ( Vsin A)t - g t2/2 (a = - g in the vertical
direction)
assuming that the ball starts at x = 0 and y = 0. The
vertical speed of the ball at any time t is given by
Vy
= Vsin A - gt
(from the formula v = u + at)
so the ball reaches its maximum height at time t =
(Vsin A)/g when Vy = 0.
The ball takes the same time to fall back to the ground, so the total travel
time in the air is 2t = 2(Vsin A)/g and the total horizontal distance travelled
(the range R) is given by
R
= (Vcos A) 2t = 2(Vcos A) (Vsin A)/g = V2 (sin 2A) / g
R is a maximum when A = 45 degrees.
7. EQUATIONS INCLUDING LIFT AND DRAG FORCES
The relevant formulas for cases where lift and drag
are important are described in our book “The Physics and Technology of Tennis”
(and in many other publications). You can download the relevant section of our
book here.