


Next: MHD approximations
Up: Fluid & MHD Theory
Previous: Fluid theory
Magnetohydrodynamic
theory involves a further simplification of fluid theory, where the
proton and electron fluids are combined and assumed
to possess a common flow velocity U.
We also assume that
the relevant time scales are long in comparison
with microscopic particle motion time scales (
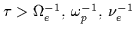 )
and that spatial scale lengths are long in comparison with the Debye length
and the thermal ion gyroradius.
The equation of motion for the MHD fluid is derived by
adding electron and proton forms of (
)
and that spatial scale lengths are long in comparison with the Debye length
and the thermal ion gyroradius.
The equation of motion for the MHD fluid is derived by
adding electron and proton forms of (![[*]](l2hicons/gif/cross_ref_motif.gif) ), to give
), to give
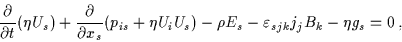 |
(3.31) |
where
pis = pp,is + pe,is = p; i.e., we assume that the
distribution of particle velocities is sufficiently random such that
pij can be approximated by a scalar.
In vector form,
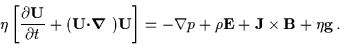 |
(3.32) |
The fluid velocity
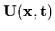 is an Eulerian
velocity, which refers
to the velocity of a fluid element, and not the the velocity of
individual particles that constitute that fluid element at any one time.
This is to be contrasted with a Lagrangian velocity, which is the
time derivative of the position vector of a particle, and is thus only
a function of time; e.g., Newton's equation of motion for
a single particle is Lagrangian.
The term
is an Eulerian
velocity, which refers
to the velocity of a fluid element, and not the the velocity of
individual particles that constitute that fluid element at any one time.
This is to be contrasted with a Lagrangian velocity, which is the
time derivative of the position vector of a particle, and is thus only
a function of time; e.g., Newton's equation of motion for
a single particle is Lagrangian.
The term 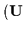
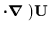 is called the
convective derivative.
is called the
convective derivative.
A further relation, linking 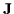 and the fields, is obtained
by multiplying the proton form of (
and the fields, is obtained
by multiplying the proton form of (![[*]](l2hicons/gif/cross_ref_motif.gif) ) by
- e/me and the electron form of (
) by
- e/me and the electron form of (![[*]](l2hicons/gif/cross_ref_motif.gif) ) by
e/mp (where e is the charge of an electron).
Terms quadratic in velocity are ignored ensuring that the
resulting expression will be linear in
) by
e/mp (where e is the charge of an electron).
Terms quadratic in velocity are ignored ensuring that the
resulting expression will be linear in 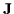 .
Adding the two
equations,
.
Adding the two
equations,
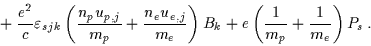 |
(3.33) |
The following simplifying approximations are made (given that
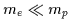 ):
):
Further, we assume that the momentum exchanged between electrons and ions is
proportional to the relative velocity of the two types of particles, with
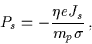 |
(3.34) |
where 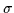 is the conductivity coefficient,
with
is the conductivity coefficient,
with
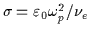 .
This gives the generalized form of Ohm's law:
.
This gives the generalized form of Ohm's law:
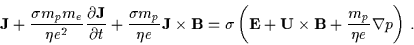 |
(3.35) |
For low-frequency disturbances, with characteristic frequency
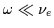 ,
the second term on the left-hand side
may be dropped. In situations where the electron cyclotron
frequency
,
the second term on the left-hand side
may be dropped. In situations where the electron cyclotron
frequency
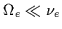 ,
the third term on the left-hand side
may also be dropped.
If the pressure gradient term is also insignificant, then (
,
the third term on the left-hand side
may also be dropped.
If the pressure gradient term is also insignificant, then (![[*]](l2hicons/gif/cross_ref_motif.gif) )
reduces to
)
reduces to
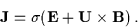 |
(3.36) |
In the
perfectly conducting limit (
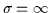 ), (
), (![[*]](l2hicons/gif/cross_ref_motif.gif) )
further simplifies to
)
further simplifies to
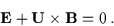 |
(3.37) |
This means that a highly conducting plasma with zero current must set up
an electric field
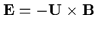 .
This is a convection
electric field that leads to
.
This is a convection
electric field that leads to
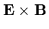 drift of the plasma
perpendicular to
drift of the plasma
perpendicular to 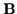 .
See Lecture 2 for examples.
Equation (
.
See Lecture 2 for examples.
Equation (![[*]](l2hicons/gif/cross_ref_motif.gif) ) also leads
to the condition of frozen-in magnetic flux
(not proven here)
in which a plasma carries a magnetic field along with it.
This condition may be stated formally as
the magnetic flux through a closed loop that moves with the fluid
is constant in time, where the magnetic flux
) also leads
to the condition of frozen-in magnetic flux
(not proven here)
in which a plasma carries a magnetic field along with it.
This condition may be stated formally as
the magnetic flux through a closed loop that moves with the fluid
is constant in time, where the magnetic flux
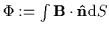 ,
where
,
where
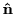 is the unit normal
to a surface
is the unit normal
to a surface 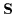 .
This is illustrated in Figure
.
This is illustrated in Figure ![[*]](l2hicons/gif/cross_ref_motif.gif) for a closed loop at two
consecutive times t1 and t2, where the loop is
stretched out as the fluid locally expands.
The density of
magnetic field lines enclosed by the loop decreases
so as to conserve magnetic flux.
The frozen-in flux condition
for a closed loop at two
consecutive times t1 and t2, where the loop is
stretched out as the fluid locally expands.
The density of
magnetic field lines enclosed by the loop decreases
so as to conserve magnetic flux.
The frozen-in flux condition
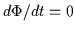 can be proven by
substituting (
can be proven by
substituting (![[*]](l2hicons/gif/cross_ref_motif.gif) ) into Faraday's Law (
) into Faraday's Law (![[*]](l2hicons/gif/cross_ref_motif.gif) ) to give
) to give
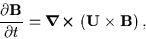 |
(3.38) |
and using Gauss's law and Stoke's theorem.
We define a magnetic flux tube to be the surface generated by moving
any closed loop parallel to the magnetic field lines it intersects
at any given time. This surface encloses a constant amount of magnetic
flux. As a consequence of flux conservation, the same fluid elements
constitute a flux tube at different times. The fluid and magnetic field lines
move together. A further consequence of the frozen-in flux condition
is that all particles initially in a flux tube will remain in the
same flux tube at later times.
Figure:
The closed loop S embedded in the fluid is stretched out at
a later time
t2>t1 by a non-uniform fluid velocity profile. The magnetic
flux through S remains constant and the field lines are tied to
the fluid.
|
An equation of energy continuity is derived by taking the
second order moment of Boltzmann's equation, to give
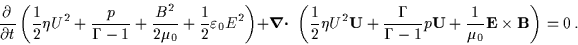 |
(3.39) |
where 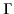 is the adiabatic index which takes the value 5/3 for
a monatomic gas.
Equation (
is the adiabatic index which takes the value 5/3 for
a monatomic gas.
Equation (![[*]](l2hicons/gif/cross_ref_motif.gif) ) assumes the
adiabatic equation of state,
for which there is no change in internal energy
of a fluid element as it propagates,
with
) assumes the
adiabatic equation of state,
for which there is no change in internal energy
of a fluid element as it propagates,
with
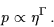 |
(3.40) |



Next: MHD approximations
Up: Fluid & MHD Theory
Previous: Fluid theory
Iver Cairns
1999-08-09
![]() )
and that spatial scale lengths are long in comparison with the Debye length
and the thermal ion gyroradius.
The equation of motion for the MHD fluid is derived by
adding electron and proton forms of (
)
and that spatial scale lengths are long in comparison with the Debye length
and the thermal ion gyroradius.
The equation of motion for the MHD fluid is derived by
adding electron and proton forms of (![]() ), to give
), to give
![]() and the fields, is obtained
by multiplying the proton form of (
and the fields, is obtained
by multiplying the proton form of (![]() ) by
- e/me and the electron form of (
) by
- e/me and the electron form of (![]() ) by
e/mp (where e is the charge of an electron).
Terms quadratic in velocity are ignored ensuring that the
resulting expression will be linear in
) by
e/mp (where e is the charge of an electron).
Terms quadratic in velocity are ignored ensuring that the
resulting expression will be linear in ![]() .
Adding the two
equations,
.
Adding the two
equations,
![]() ), (
), (![]() )
further simplifies to
)
further simplifies to