


Next: MHD waves
Up: Fluid & MHD Theory
Previous: Final MHD equations
The magnetic force (per unit volume) in the equation for
fluid motion (![[*]](l2hicons/gif/cross_ref_motif.gif) ) may be re-expressed as
) may be re-expressed as
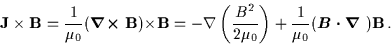 |
(3.46) |
The first term corresponds to the magnetic pressure,
with
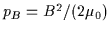 .
An important diagnostic of a plasma is the plasma beta, defined
as the ratio of plasma thermal pressure to the magnetic pressure:
.
An important diagnostic of a plasma is the plasma beta, defined
as the ratio of plasma thermal pressure to the magnetic pressure:
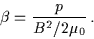 |
(3.47) |
The second term can be further decomposed into two terms:
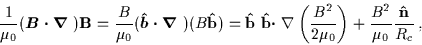 |
(3.48) |
where
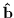 is a unit vector in the direction of
is a unit vector in the direction of 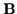 and
and
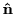 is the normal pointing towards the centre of curvature,
defined by (
is the normal pointing towards the centre of curvature,
defined by (
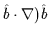
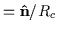 ,
where Rc is the radius of curvature of the field
line. The first term cancels out the magnetic pressure
gradient term in (
,
where Rc is the radius of curvature of the field
line. The first term cancels out the magnetic pressure
gradient term in (![[*]](l2hicons/gif/cross_ref_motif.gif) ) in the
direction along the field lines. This
implies that the magnetic pressure force is not isotropic;
only perpendicular components of
) in the
direction along the field lines. This
implies that the magnetic pressure force is not isotropic;
only perpendicular components of
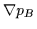 exert force on the
plasma.
The second term in (
exert force on the
plasma.
The second term in (![[*]](l2hicons/gif/cross_ref_motif.gif) )
corresponds to the magnetic tension force which is directed
towards the centre of curvature of the field lines and thus acts to
straighten out the field lines. A suitable analogy is the tension force
transferred to
an arrow by the stretched string of a bow. In this case the
tension force pushes the plasma in the direction that will reduce
the length of the field lines.
)
corresponds to the magnetic tension force which is directed
towards the centre of curvature of the field lines and thus acts to
straighten out the field lines. A suitable analogy is the tension force
transferred to
an arrow by the stretched string of a bow. In this case the
tension force pushes the plasma in the direction that will reduce
the length of the field lines.



Next: MHD waves
Up: Fluid & MHD Theory
Previous: Final MHD equations
Iver Cairns
1999-08-09
![]() ) may be re-expressed as
) may be re-expressed as