


Next: Further Reading:
Up: Fluid & MHD Theory
Previous: Magnetic pressure and tension
For low-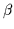 plasmas, with
plasmas, with
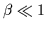 (also referred to as cold
plasmas) the stresses in the plasma are predominantly magnetic.
We seek MHD wave solutions in a cold magnetized plasma.
In treating small-amplitude waves, the MHD equations are linearized,
keeping only terms linear in the amplitude of the wave
(
(also referred to as cold
plasmas) the stresses in the plasma are predominantly magnetic.
We seek MHD wave solutions in a cold magnetized plasma.
In treating small-amplitude waves, the MHD equations are linearized,
keeping only terms linear in the amplitude of the wave
(
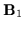 ,
,
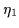 ,
and
,
and
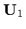 ).
We seek plane wave solutions; i.e., solutions that vary in space and
time as
).
We seek plane wave solutions; i.e., solutions that vary in space and
time as
![${\rm exp}[-i(\omega t - k x)]$](img117.gif) (assuming that the plane wave propagates
in the x-direction, with
(assuming that the plane wave propagates
in the x-direction, with
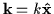 ).
Additional assumptions are that the background magnetic field
).
Additional assumptions are that the background magnetic field
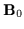 and plasma density
and plasma density 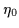 are uniform, that there are no
background
currents or electric fields, and that there is
no bulk fluid motion.
Our starting equations are:
are uniform, that there are no
background
currents or electric fields, and that there is
no bulk fluid motion.
Our starting equations are:
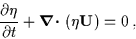 |
(3.49) |
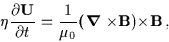 |
(3.50) |
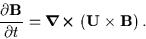 |
(3.51) |
After linearizing, and replacing the time and spatial derivatives
by
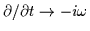 and
and
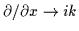 ,
these equations become
,
these equations become
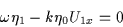 |
(3.52) |
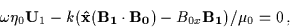 |
(3.53) |
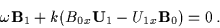 |
(3.54) |
Without loss of generality we assume that
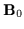 lies in the
x-z plane, with
lies in the
x-z plane, with
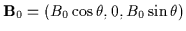 ,
where
,
where 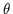 is the angle between
is the angle between
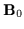 and
and 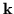 .
After eliminating
.
After eliminating
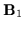 from (
from (![[*]](l2hicons/gif/cross_ref_motif.gif) ) and (
) and (![[*]](l2hicons/gif/cross_ref_motif.gif) ),
the three equations relating components of
),
the three equations relating components of
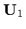 are
written in the following matrix form:
are
written in the following matrix form:
![\begin{displaymath}\left[
\begin{array}{ccc}
\left( {\omega^{2}}/{k^{2}} - v_{A}...
... U_{1x} \\ U_{1y} \\
U_{1z}
\end{array}\right] = {\bf0} \, ,
\end{displaymath}](img131.gif) |
(3.55) |
where the Alfvèn velocity vA satisfies
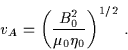 |
(3.56) |
A solution for
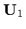 exists only if the determinant of this
matrix vanishes. This yields two independent non-trivial solutions for
exists only if the determinant of this
matrix vanishes. This yields two independent non-trivial solutions for 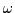 as a function of k (known as the dispersion relation):
as a function of k (known as the dispersion relation):
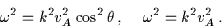 |
(3.57) |
The first solution corresponds to Alfvèn waves. After substituting the
dispersion relation back into the matrix equation (![[*]](l2hicons/gif/cross_ref_motif.gif) ),
we find that a solution for
),
we find that a solution for
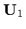 is only possible if
U1x = U1z = 0. Thus Alfvèn waves are shear waves
that shift plasma in the direction perpendicular
to the plane containing the wavevector
is only possible if
U1x = U1z = 0. Thus Alfvèn waves are shear waves
that shift plasma in the direction perpendicular
to the plane containing the wavevector 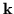 and the background magnetic field
and the background magnetic field
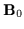 ,
and
that propagate with a phase velocity
,
and
that propagate with a phase velocity
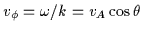 .
The wave motion in an Alfvèn wave may be attributed to
an interplay between magnetic tension and plasma inertia. When a fluid
element is displaced relative to
.
The wave motion in an Alfvèn wave may be attributed to
an interplay between magnetic tension and plasma inertia. When a fluid
element is displaced relative to
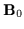 the magnetic field is
displaced with the fluid. The field line becomes locally curved, which
generates a tension force tending to straighten out the field line. The
inertia of the plasma causes it to overshoot, setting up an oscillatory
motion.
The density of the fluid is
unaffected by the propagating Alfvèn wave [
the magnetic field is
displaced with the fluid. The field line becomes locally curved, which
generates a tension force tending to straighten out the field line. The
inertia of the plasma causes it to overshoot, setting up an oscillatory
motion.
The density of the fluid is
unaffected by the propagating Alfvèn wave [
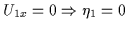 in (
in (![[*]](l2hicons/gif/cross_ref_motif.gif) )].
The group velocity (velocity at which information propagates and the
direction for energy flow) for Alfvèn waves satisfies
)].
The group velocity (velocity at which information propagates and the
direction for energy flow) for Alfvèn waves satisfies
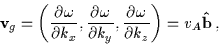 |
(3.58) |
so that the flow of energy associated with Alfvèn waves is directed
along the background magnetic field direction.
The dispersion relation
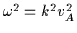 corresponds to
the magnetoacoustic mode.
Substituting the dispersion relation into (
corresponds to
the magnetoacoustic mode.
Substituting the dispersion relation into (![[*]](l2hicons/gif/cross_ref_motif.gif) ) yields
the requirement that U1y=0 (for
) yields
the requirement that U1y=0 (for
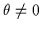 ), so that the
fluid motion is in the plane containing
), so that the
fluid motion is in the plane containing 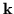 and
and
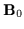 .
Because U1x is not required to be zero, (
.
Because U1x is not required to be zero, (![[*]](l2hicons/gif/cross_ref_motif.gif) ) implies
that
) implies
that 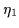 is also nonzero; i.e., magnetoacoustic waves affect the
plasma density and are thus called compressional waves.
For magnetoacoustic waves,
is also nonzero; i.e., magnetoacoustic waves affect the
plasma density and are thus called compressional waves.
For magnetoacoustic waves,
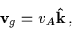 |
(3.59) |
so that wave energy may flow at an arbitrary angle to
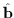 ,
as opposed to
Alfvèn waves (with
,
as opposed to
Alfvèn waves (with
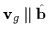 ).
).
In a warm plasma,
when 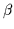 is no longer small relative to unity, the plasma
pressure terms can no longer be ignored.
The pressure gradient term is reinserted in (
is no longer small relative to unity, the plasma
pressure terms can no longer be ignored.
The pressure gradient term is reinserted in (![[*]](l2hicons/gif/cross_ref_motif.gif) )
and the adiabatic
equation of state (
)
and the adiabatic
equation of state (![[*]](l2hicons/gif/cross_ref_motif.gif) ) closes the set of equations.
In this case a linear analysis yields a dispersion relation
with three solutions:
) closes the set of equations.
In this case a linear analysis yields a dispersion relation
with three solutions:
![\begin{displaymath}\omega^{2} = k^{2} v_{A}^{2} \cos^{2} \theta \, , \,\,\,\,\,\...
...^{2}-4v_{A}^{2} c_{S}^{2}
\cos^{2} \theta ]^{\frac{1}{2}} \, ,
\end{displaymath}](img143.gif) |
(3.60) |
with the sound speed
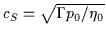 .
These three solutions correspond to the Alfvèn mode, and the
fast (+) and slow (-) magnetoacoustic modes, so named
because the phase speeds satisfy
.
These three solutions correspond to the Alfvèn mode, and the
fast (+) and slow (-) magnetoacoustic modes, so named
because the phase speeds satisfy
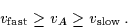 |
(3.61) |
In the limit of small background magnetic field strengths, fast mode waves
become gas sound waves, with the dispersion relation
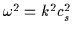 .
In the cold plasma limit, fast mode waves become
magnetoacoustic waves.
In the small-field limit, slow mode waves become magnetoacoustic-like,
with the dispersion relation
.
In the cold plasma limit, fast mode waves become
magnetoacoustic waves.
In the small-field limit, slow mode waves become magnetoacoustic-like,
with the dispersion relation
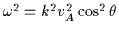 .
These
only have magnetoacoustic properties for small angles
.
These
only have magnetoacoustic properties for small angles 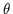 .
In the cold plasma limit, slow mode waves (along the field lines)
become gas-sound-like, with
.
In the cold plasma limit, slow mode waves (along the field lines)
become gas-sound-like, with
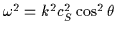 .
.



Next: Further Reading:
Up: Fluid & MHD Theory
Previous: Magnetic pressure and tension
Iver Cairns
1999-08-09
![]() plasmas, with
plasmas, with
![]() (also referred to as cold
plasmas) the stresses in the plasma are predominantly magnetic.
We seek MHD wave solutions in a cold magnetized plasma.
In treating small-amplitude waves, the MHD equations are linearized,
keeping only terms linear in the amplitude of the wave
(
(also referred to as cold
plasmas) the stresses in the plasma are predominantly magnetic.
We seek MHD wave solutions in a cold magnetized plasma.
In treating small-amplitude waves, the MHD equations are linearized,
keeping only terms linear in the amplitude of the wave
(
![]() ,
,
![]() ,
and
,
and
![]() ).
We seek plane wave solutions; i.e., solutions that vary in space and
time as
).
We seek plane wave solutions; i.e., solutions that vary in space and
time as
![]() (assuming that the plane wave propagates
in the x-direction, with
(assuming that the plane wave propagates
in the x-direction, with
![]() ).
Additional assumptions are that the background magnetic field
).
Additional assumptions are that the background magnetic field
![]() and plasma density
and plasma density ![]() are uniform, that there are no
background
currents or electric fields, and that there is
no bulk fluid motion.
Our starting equations are:
are uniform, that there are no
background
currents or electric fields, and that there is
no bulk fluid motion.
Our starting equations are:
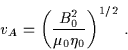
![]() corresponds to
the magnetoacoustic mode.
Substituting the dispersion relation into (
corresponds to
the magnetoacoustic mode.
Substituting the dispersion relation into (![]() ) yields
the requirement that U1y=0 (for
) yields
the requirement that U1y=0 (for
![]() ), so that the
fluid motion is in the plane containing
), so that the
fluid motion is in the plane containing ![]() and
and
![]() .
Because U1x is not required to be zero, (
.
Because U1x is not required to be zero, (![]() ) implies
that
) implies
that ![]() is also nonzero; i.e., magnetoacoustic waves affect the
plasma density and are thus called compressional waves.
For magnetoacoustic waves,
is also nonzero; i.e., magnetoacoustic waves affect the
plasma density and are thus called compressional waves.
For magnetoacoustic waves,
![]() is no longer small relative to unity, the plasma
pressure terms can no longer be ignored.
The pressure gradient term is reinserted in (
is no longer small relative to unity, the plasma
pressure terms can no longer be ignored.
The pressure gradient term is reinserted in (![]() )
and the adiabatic
equation of state (
)
and the adiabatic
equation of state (![]() ) closes the set of equations.
In this case a linear analysis yields a dispersion relation
with three solutions:
) closes the set of equations.
In this case a linear analysis yields a dispersion relation
with three solutions: