PHYSICS OF BOUNCE

Rod Cross, Physics Dept, Sydney University Updated June 2014

The photo above shows the footprint of a high speed rubber ball incident from the left on chalk on a blackboard. The ball slides at the start of the bounce and sweeps away the chalk. It then grips the board and rolls over the chalk. The two dashed lines on the board are 100 mm apart.

Click the photo to see a fascinating series of bounces of a spinning superball, filmed in slow motion. It is mesmerizing. The ball retraces its incident path when it bounces on the right hand side of the table. The ball grips the table during each bounce and reverses both its direction of motion and the spin direction. There is a lot of interesting physics in both of these events.

A fundamental physics problem in ball sports is to measure or calculate the way the ball bounces. The following diagram illustrates the problem. If a ball is incident at a certain speed and angle on a surface, then how fast does it bounce, at what angle, and with how much spin?

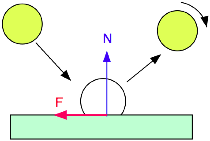
The problem is more complicated than one might expect. There is a vertical force N, called the normal reaction force, which acts to change the vertical speed of the ball, and there is a horizontal friction force, F, that acts to change the horizontal speed of the ball. In addition, F exerts a torque on the ball that changes its rotation speed. If N acts along a line that does not pass through the middle of the ball, then N also exerts a torque on the ball.

If the ball slides throughout the bounce then F/N = coefficient of sliding friction. But that happens only if the ball is incident at a glancing angle to the surface, typically about 20 degrees or less. At larger angles of incidence, the bottom of the ball will come to a stop before the ball bounces, and grip the surface, in which case static friction acts on the ball. F is then determined by elastic distortion of the ball in a direction parallel to the surface, and acts as a shear force. F can even reverse direction during the bounce.

The simplest way to determine how the ball bounces is to film the bounce and then measure what happens from the film. The ratio of the vertical speed after the bounce to that before the bounce is called the COR (Coefficient of Restitution). We can also define a horizontal COR in an analogous way, in terms of the horizontal speed of the contact point at the bottom of the ball. The horizontal speed at the bottom of the ball depends on how fast the ball is spinning, as well as on the horizontal speed of the centre of mass of the ball. A superball has a horizontal COR about 0.5 or 0.6, whereas most other balls have a lower horizontal COR, typically about 0.1 or 0.2. The vertical and horizontal COR also depend on the elastic properties of the surface. For example, if the surface is rubber rather than concrete then the horizontal COR will be larger and the ball will spin faster after it bounces.

GRIP DURING BOUNCE

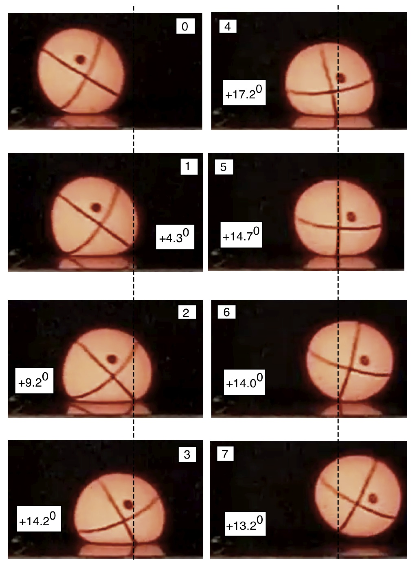
The following images were taken from video film of a hollow rubber ball incident obliquely on a smooth block of granite. The ball was filmed at 1200 frames/sec. The vertical dashed lines pass through a fixed point on the granite surface. Equator lines were drawn on the ball to measure its rotation during the bounce. The images show two interesting results. The first is that the bottom of the ball gripped the surface during most of the bounce. The bottom of one equator line remained firmly attached to the dashed lines, rather than sliding forwards. The ball moved forwards like a bulldozer or an army tank on catterpillar track. The second is that the ball first leans forward in frames 1 and 2, due to its high initial speed, then it leans backwards in frame 4. The ball therefore vibrates sideways, and causes the friction force on the bottom of the ball to reverse direction. As a result, the ball spin at first increases during the bounce then it decreases. The angle shown in each frame is the change in rotation angle from one frame to the next.

BOUNCE FILM

Baseball bounce (At 1000 f/s) Tennis ball bounce (At 1000 f/s)

Superball 1000 f/s (note spin reversal)

TENNIS BALL at 3000 f/s incident at 30 m/s on clay and on grass (copyright by ITF). Can be viewed with QuickTime or RealPlayer and is in H.264 compressed format. Note how clay sticks to the ball and is then spun off. The grass here was longer than normally seen at Wimbledon. Grass is a faster surface than clay, even when the grass is long. You can work out the bounce speed, spin and angle yourself from this film.

HOOP Bounce1, Bounce2, Bounce3 at 600 fps (taken with a Casio EX-F1 camera).

The hoop slides then grips before bouncing, in the same but in a much more obvious manner than a ball. It is also obvious, especially in bounce2, that the normal reaction force does not act through the centre of mass and therefore exerts a strong torque on the hoop, reducing the spin rate. The same effect occurs with spherical balls. If one part of a ball stops rotating while the rest of the ball continues to rotate, what then happens to the ball? The hoop film here helps to answer that question. The hoop behaves as a system of inter-connected particles rather than as a rigid object. The angular momentum of the system is well-defined, even though the angular velocity and moment of inertia are not.

TENNIS STRINGS at 600 fps with 25 m/s tennis ball incident on a hand-held racquet. Four different strings showing string movement: String1 String2 String3 String4. You need to advance one frame at a time to see the movement. Note that strings return to their original position very quickly, at least when new, thereby enhancing the spin of the outgoing ball (as explained in the pretty picture below). That’s why Hewitt has stopped fiddling with his strings so much between points.

BOUNCE OFF A FLEXIBLE SURFACE

This is a pretty picture of a golf ball and an 8mm thick slice of a large superball sitting on a slab of polished granite. The ball spins faster when it bounces off the superball slice since the tangential coefficient of restitution is much larger. A golf ball that spins faster will travel further. Click on photo to see a simplified explanation of why the ball spins faster. The same effect occurs with tennis strings.

SUPERBOUNCES (Oct 2007, Dec 2009)

A popular physics demonstration is to drop two balls together, say a tennis ball on top of a basketball. The tennis ball then bounces with about 16 times more energy, by bouncing off the basketball, than it does by bouncing directly off the floor. A common, simplified explanation is that the basketball bounces first and then makes a second collision with the incoming tennis ball. In fact, both balls bounce together (unless the tennis ball is deliberately or accidentally dropped shortly after the basketball). See for yourself, at 300 frames/sec, here.

A detailed explanation of the process involved is given in American Journal of Physics, 75, 1009-1016 (2007). If the bigger ball is on top, then the small ball gets trapped between the big ball and the floor and can bounce many times before the two balls separate. A movie is shown here, but the multiple bounces can’t be seen in the movie since they happen too quickly. They can be seen much more easily by bouncing the balls off a piezo disk or force plate, as described in the AJP paper.

SPRING BOUNCE (Jan 2008, Nov 2009)

When a ball bounces, the force on the ball increases to a maximum when the ball compression is a maximum, and then drops back to zero at the end of the bounce period. The force varies in a sinusoidal manner. When a spring bounces on its end, the force remains constant in time while a compression wave travels up to the top end, reflects, and travels back to the bottom end. Then the force drops to zero and the spring bounces. A 300 frames/sec movie showing the compression wave can be seen here (taken in sunlight with a Casio EX-F1 camera using 1/4000s exposure). The bounce is also shown in the diagram below. The movie is played back at 30 fps (in slow motion). Note also that the bottom of the spring starts falling well AFTER the top is released!

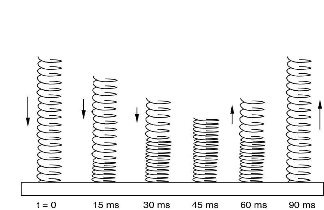
An interesting feature is that the spring bounces after the wave makes two trips (one up and one down) along the spring. When a steel ball bounces, a compression wave travels up and down the ball about 15 times before the ball bounces. The force on the ball is not constant like it is for a spring since it takes a long time for the bottom of the ball to compress and then expand.

When two springs or two rods collide, and if the lengths are different, then kinetic energy is not conserved since the long rod or the long spring is still compressed at the end of the collision. When two steel balls collide, kinetic energy is conserved even if the balls are of different diameter. The reason is that wave motion during a collision between two balls plays a neglible role. Almost all the elastic energy in the two balls is stored in the small contact volume and very little energy is coupled to propagating waves since the collision is spread out over a long time. The collision takes a long time because the contact area is quite small and relatively soft compared with the rest of the ball. The difference between ball and spring collisions is described in more detail here.

SLINKY DROP (Jan 2008, Nov 2009)

When a slinky spring is suspended at its top end and then released, will the whole spring fall vertically as soon as the top end is released? Or will the bottom end fall first? Or will the top end fall first? Think it through then check your answer here (filmed at 300 frames/sec). It’s quite surprising. See Am. J. Phys. p 583 - 587, July 2007 for an explanation.

A similar thing happens when a player strikes a ball with a bat or club or racquet. The impact sends a transverse wave along the implement, but the ball is well on its way by the time the bending wave arrives at the player’s hands. So, anything fancy the player does with the hands during or after striking the ball is purely for show. The only role of the hands after the impact is to bring the implement to a stop.

ODD-BALL BOUNCES

Most balls used in sport are spherical. Some are elongated, like oval shaped footballs. They are subject to the same ground reaction and friction forces as any other ball, but the normal reaction force rarely acts through the centre of mass of the ball. This results in a novel bounce effect whereby elongated balls tend to bounce in the direction they are pointing when they hit the ground. To study this effect, I made a fat pencil from a plastic tube with an eraser stuck in one end. The bounce of such an object can be quite amusing, as shown in the attached movie. The bounce of such an object shows clearly that static friction is often more important than sliding friction during the bounce. Sliding friction can bring an object to rest in the sliding direction but it can’t reverse the direction of motion and it can’t accelerate an object in the sliding direction. Only static friction can do that.

The plus sign on the pencil marks its centre of mass and the vertical white line in the middle of the film is a plumbob. The movie is not very entertaining when viewed in real time. You need to advance it one frame at a time to slow it down.

Falling pencils (or trees or chimneys) can also behave in unexpected ways, as shown in this movie and as described in this paper.

FOOTBALL BOUNCE

Footballs tend to bounce in the direction they are pointing when they land, as shown in MovieA. This is not always the case, since the bounce direction also depends on the spin, the direction of the spin and the initial forward speed. MovieB shows the unexpected nature of some football bounces. These two movies were filmed at 25 frames/s but each frame was split in half. The top half was recorded 10 ms before the bottom half, the time interval between each frame being 40 ms in both halves of the movie. Other bounces are shown on the Movie Clips page.

A scientific paper on this subject, including the results of 200 different bounces at various angles and spins, can be downloaded as a 700 kb pdf file.

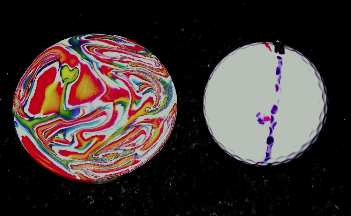
STRESS IN A BOUNCING BALL

Maximum stress in a ball occurs in the small region where the ball contacts the surface. A rough indication of the stress pattern is shown in the following photos of a 1 mm thick sheet of polycarbonate compressed edge-on (top to bottom) and viewed through two sheets of crossed polaroid. The polycarbonate sheet was cut with scissors to have a flat surface at the top and a curved surface at the bottom.

The stress is obviously concentrated in the contact region but extends around the edge of the sheet as the compression force increases due to bending of the polycarbonate sheet. The photos were taken in room light with a sheet of white cardboard at the rear to reflect light through the system. The polycarbonate sheet is between two large sheets of polaroid.

BOUNCE WITH TWO SPRINGS

It is not easy to see by eye what happens to a ball when it bounces.

Here are three bounces using two springs under a brass bar to catch the action: